| 木星雲対流モデルの開発 | << Prev | Index| Next >> |
力学的枠組みとして, 準圧縮方程式系 [1] を用いる. この方程式系では変数を水平一様な静水圧平衡した基本場とそこからの擾乱に分離し, 擾乱の時間発展方程式を解く.
運動量と圧力の擾乱に対する方程式の導出にあたっては, 凝結性成分も考慮した状態方程式を用いる必要がある.
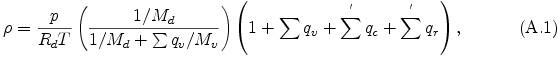
ここで, ρ は密度, p は圧力, Rd は乾燥成分に対する気体定数, T は温度, Md と Mv は それぞれ乾燥成分と凝結成分の分子量である. qv は凝結性成分気体の混合比, qc と qr は凝結物の雲と雨の混合比である. ∑ は蒸気について和を取り, ∑' は凝結物について和をとることを意味する. (A.1) 式より, エクスナー関数 π は以下のように表される.
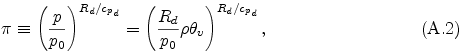
ここで, p0 は基準状態での圧力, cpd は乾燥成分気体の比熱, θv は仮温位であり,
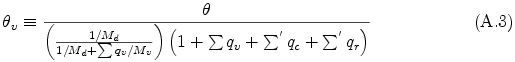
で定義される. 但し, 温位 θ は θ = T / πで定義される.
この力学的枠組みでは温位を用いるために, 比熱の温度と組成に対する依存性が無視されている. しかし, 運動構造を支配する雲層での静的安定度 N2 の値は比熱を無視しなかった場合とほとんど変わらない (補遺 G 参照).
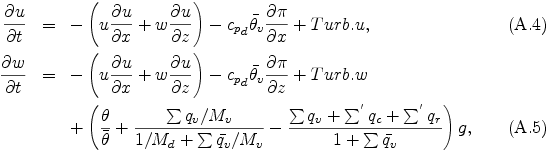
ただし u は速度の x 成分, w は速度の z 成分, g は重力加速度, Turb.u および Turb.w は乱流拡散項で, その具体的な表現は 補遺 Cに記述する. また, - の付いた変数は水平一様な基本場の値である.
圧力方程式は, 連続の式
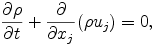
(A.1)--(A.3) 式, および後述する熱力学の式 (A.7) 式より導かれる.
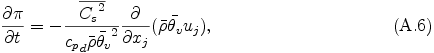
ここで Cs2 = cpd Rdπ &thetav /cvd は音速の自乗である. Klemp and Wilhelmson (1978) [1] と同様に, 非断熱加熱による大気の膨張に伴う圧力変化は小さいものとしてその項を無視している.
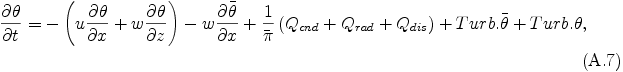
ここで Qcnd は凝結加熱項であり, その具体的な表現は補遺 Bに記述する. Qrad は放射加熱項である. Qdis と Turb.θ はそれぞれ乱流拡散項と散逸加熱項であり, その具体的な表現は補遺 C に記述する.
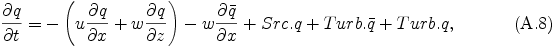
ここで Src.q は生成項<, Turb.q は乱流拡散項であり, それぞれの具体的な表現は補遺 Bと補遺 Cに記述する.
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |