木星雲対流モデルの開発	<< Prev | Index| Next >>

---

B. 熱力学的枠組みと雲微物理過程モデル

(A.7) 式中の凝縮加熱項 Q_cnd, および (A.8) 式中の生成項 Src は, Kessler (1969) ^[2] の暖かい雨のバルクパラメタリゼーション に従って評価する. このパラメタリゼーションでは 図 2.1 に示したように, 凝結成分を「蒸気」, 「雲」, 「雨」の 3 つのカテゴリに分ける. 「雲」と「雨」は共に凝結物であるが, 「雲」は大気とともに運動するのに対し, 「雨」は大気の運動から離脱して落下するものとする. 異なるカテゴリ間の変換率はそれぞれのカテゴリの混合比を用いて計算する. 簡単のために, 雲と雨のカテゴリは純物質から成るものとし, 溶液は考慮しない. さらに凝結物である H₂O 氷, NH₄SH 固体, NH₄SH 氷の間で相互作用は生じないとものと仮定する.

(A.7) 式中の凝縮加熱項 Q_cnd は各凝結成分に対して以下のように表される.

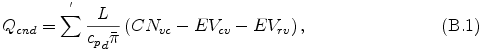
ここで L は潜熱もしくは反応熱, CN_vc は凝結による水蒸気から雲への変換率, EV_cv は蒸発による雲から水蒸気への変換率, EV_rv は蒸発による雨から水蒸気への変換率を表す. (A.8) 式中の生成項 Src は蒸気("vapor"), 雲("cloud"), 雨("rain")に対して以下のように表現できる.

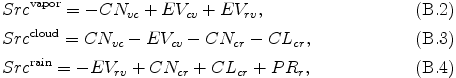
ここで CN_cr は併合成長による雲から雨への変換, CL_cr は衝突併合による雲から雨への変換を表す. (B.1) -- (B.4) 式を (A.7) 式と (A.8) 式に代入することで, (A.7) 式と (A.8) 式は以下のように表される.

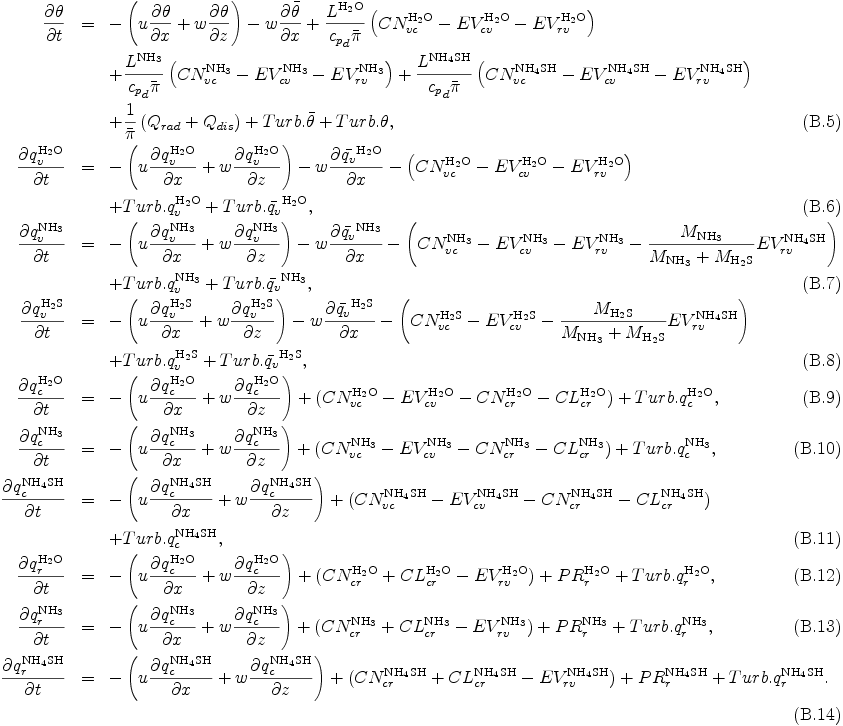
式 (B.5)--(B.14) の雲微物理に関する各項の具体的な表現は以下に示す.

雲水の併合成長: CN_cr

併合成長による雲から雨の変換率は以下の式で表す.

変換の時間スケール τ₀ と 閾値 q⁰ は, Nakajima et al. (2000) ^[6] に従いそれぞれ τ₀ = 100 sec, q⁰ = 0 とした. これらの値は木星の雨の終端速度は地球大気での値よりも大きいという効果 ^[15] を考慮して選択した.

雲水の衝突併合: CL_cr

衝突併合による雲から雨への変換率は以下の式で表す.

ここで f_j は木星重力と地球重力の比で, f_j = 3 とする ^{[6], [15]}.

雨水の蒸発: EV_rv

蒸発による雨から蒸気への変換率は過飽和量 q_vsw - q_v に比例するように与える.

雨水のフラックス: PR_r

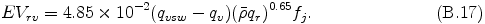
重力落下による雨水混合比の変化率は以下の式で与える.

ここで雨水の終端落下速度 U_r [m s^-1] は以下の式で与える.

蒸気と雲水の間での凝結と蒸発: CN_vc, EV_cv

蒸気と雲の間の凝結と蒸発は, Klemp and Wilhelmson (1978) ^[1] と同様に, 式 (B.5)--(B.14) から - CN_vc + EV_cv を除いた方程式系を解いた後に, 必要に応じて θ, q_v, q_c を飽和状態に調節することで評価する.

以下では予報方程式 (A.4)--(A.8) および式 (B.5)--(B.14) から - CN_vc + EV_cv を除いた場合に得られる変数に添字 ^* を付けて θ^*, q_v^*, q_c^* と表し, 調節後の変数を θ, q_v, q_c と表す.

凝結と蒸発

熱力学第一法則より, 調節前後の変数の間に以下の関係が成立する.

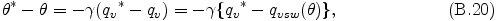
ここで調節後の蒸気の混合比 q_v は 飽和混合比 q_vsw に等しいものとする. また, γ = L_v/c_p π である. q_vsw は 補遺 F に示した H₂O と NH₃ に対する飽和蒸気圧と潜熱を用いて与える. q_vsw を θ^* のまわりでテーラー展開し, (θ^* - θ) の 2 次以上の項を無視すると, (B.20) 式は以下のような関係式に近似できる.

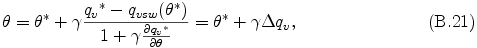
ここで

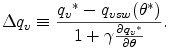
(B.21) 式より, 凝結量 CN_vc と蒸発量 EV_cv はそれぞれ,

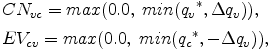
と表現される. なぜならば, 調節後の混合比は負になることはなく, さらに CN_vc と EV_cv は それぞれ正の量として定義されているからである.

これにより調節後の θ, q_v, q_c が以下の式より得られる.

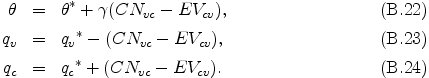
飽和状態により正確に収束させるために, 本モデルでは上記の手続きを 4 回繰り返す.

NH₄SH の生成反応

調節後の H₂S, NH₃ の分圧は NH₄SH 生成反応, NH₃ + H₂S ↔ NH₄SH, の平衡条件を満たさねばならない. 平衡定数は以下のように与えられる.

ここで p_NH3 と p_H2S はそれぞれ NH₃ と H₂S の分圧である (K_p の具体的な表現は補遺 Fを参照 のこと). NH₄SH の生成にともなう分圧の変化を Δp_NH4SH とすると, (B.25) 式は以下のように表される.

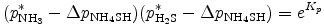
もしくは,

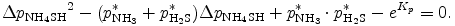
この式を解くことで Δ p_NH4SH が得られる.

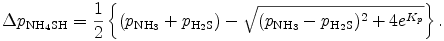
ただし, 根号の負の符号は Δ q_NH4SH < p_H2S , Δ q_NH4SH < p_H2S となるように選択した. 以上より CN_vc と EV_cv はそれぞれ,

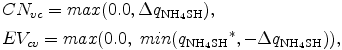
と書ける. なぜならば, 調節後の混合比が負になることはなく, さらに CN_vc と EV_cv は それぞれ正の量として定義されているからである. 混合比変化 Δ q_NH4SH は Δ p_NH4SHより計算される.

したがって調節後の θ, q_NH3, q_H2S, q_NH4SH は以下の式より得られる.

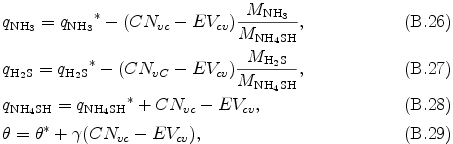
ただし, M_NH3, M_H2S, M_NH4SH はそれぞれ, NH₃, H₂S, NH₄SH の分子量である. 平衡状態へより正確に収束させるために, 本モデルでは上記の手続きを 4 回繰り返す.

---

木星雲対流モデルの開発	<< Prev | Index| Next >>