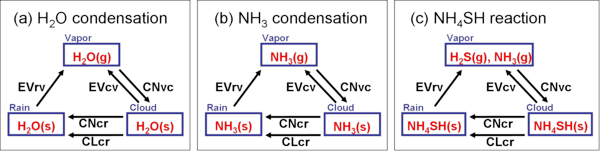
|
| 図2.1: H2O の凝結, NH3 の凝結, NH4SH の生成反応に対する雲微物理素過程. CNvc は凝結による水蒸気から雲水への変換, EVcv は蒸発による雲から水蒸気への変換, EVrv は蒸発による雨から水蒸気への変換, CNcr は併合成長による雲から雨への変換, CLcr は衝突併合による雲から雨への変換, を意味する. |
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |
基礎方程式として, 準圧縮方程式系 [1] に凝結性成分の保存式を組み合わせたものを用いる. 広い計算領域を確保した計算を実行し易くするために, 系は水平鉛直の 2 次元とする. 定式化の詳細は 補遺 A を参照されたい.
この方程式系に基づいた数値計算コードは, Nakajima et al. (2000) [6], の採用した非弾性方程式系に基づく数値計算コードに比べると, 楕円型偏微分方程式を解く必要がないため, 領域分割による並列化を用いた大領域計算に適しており, 2 次元モデルから 3 次元モデルへの拡張に適している. また, 準圧縮系は, 音速を基本場での値で代換えすることで 完全圧縮系に比べて計算コストの増大を少なくした近似方程式系である [8] これらの理由により 準圧縮系方程式は近年の地球大気の雲対流モデルにしばしば採用されてきた.
大気は H2, He, H2O, NH3, H2S から成るものとし, それぞれ理想気体の状態方程式に従うものと仮定する. H2 と He は非凝結成分として扱い, H2O, NH3, H2S は凝結成分として扱う. 相変化と化学反応として以下を考慮する.
凝結と化学反応に伴う熱の出入りを熱力学の式において考慮する. 凝結物は大気とともに運動し落下しない「雲」と, 大気の運動から離脱して落下する「雨」に区分する. 簡単のために, 雲と雨は純物質から成るものとし, 溶液の存在は考慮しない.
カテゴリ間の変換は, 地球の雲モデルで利用されている Kessler (1969) [2] のパラメタリゼーションを用いて表現する. このパラメタリゼーションでは, 図 2.1 に示される雲微物理素過程を考慮し, カテゴリ間の変換速度を定めている. このパラメタリゼーションは通常, 固相が関与しない「暖かい雨」を想定したものとされており, 固相と液相の両方が存在する可能性がある木星大気にどの程度有効かは自明ではない. しかし本研究では, 単純でよく利用されているパラメタリゼーションであるという理由から, Kessler (1969) [2] のパラメタリゼーションを用いることにした. 詳細は補遺 B を参照されたい.
モデル格子間隔以下のスケールを持つ乱流による拡散は, Klemp and Wilhelmson (1978) [1] のパラメタリゼーションにしたがって計算する. このパラメタリゼーションは, サブグリッドスケールの運動エネルギーの予報方程式を解くことで, 乱流拡散係数を決めるものである. 詳細は補遺 C を参照されたい.
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |