| 木星雲対流モデルの開発 | << Prev | Index| Next >> |
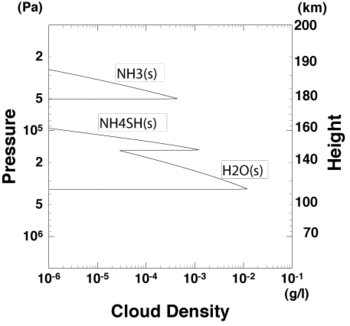
木星大気には, 大気中の対流運動によって 3 層の雲が存在すると予想されている. すなわち, 最上部に NH3 氷の雲層, 中間に NH4SH 固体の雲層, 最下層に H2O 氷の雲層である[3],[4] (図 1.1 参照). 彼らの示した雲の鉛直分布は標準的な分布として受け入れられているが, 上昇する気塊とその熱平衡を仮定した鉛直 1 次元の熱平衡計算によって見積もられたものである. 彼らの計算では移流等の対流運動と降水等の雲微物理過程は考慮されていない.
雲の生成消滅は対流運動と雲微物理過程の影響を受けるだけでなく, 大気の成層構造の決定を通して対流運動それ自身に影響を与える. 雲の生成消滅と対流運動を陽に扱い, それらの関係を議論した従来の木星大気研究としては, Nakajima et al. (2000)[6] がある. 彼らは凝結性成分として H2O に着目し, その相変化と雲微物理過程を考慮した 2 次元の数値対流モデル (以下, 雲対流モデル) を用いて長時間積分を実行することにより, 統計的平衡状態での対流運動の様相, および平均的な温度, 雲, 蒸気の鉛直分布を調べた. 彼らは H2O 凝結高度に形成される安定層が対流運動に対する境界として働き, その高度を境に対流運動が上下に分割されることを示した. Nakajima et al. (2000)[6] が考慮しなかった NH3 の凝結ならびに NH4SH の生成においても同様の安定層の形成が示唆されている. 熱平衡モデルを用いた成層安定度の評価 [7] によれば, その強度 (浮力振動数) は H2O の凝結高度での安定度と同じオーダーに達することが予想されている. したがって, H2O 凝結高度で見られたような対流運動の分 割が他の 2 つの凝結高度においても生じ, 平均的な鉛直雲分布に影響を与え る可能性がある.
このような背景の下, 本研究では, 対流運動を考慮することで得られる木星大気中の平均的な鉛直雲分布と流れ場の様相を明らかにすることを目指し, 関与する主要凝結性成分のすべてを考慮することのできる雲対流モデルの開発を行う. 統計的な平均状態を得るに必要となる大領域長時間積分の実行を可能とするために Nakajima et al. (2000)[6] と同様, 流体運動を 2 次元に限定した対流モデルとするが, 流体運動の基礎方程式は Nakajima et al. (2000)[6] が用いた非弾性系ではなく, 大領域化したとき, あるいは, 将来 3 次元化したときに計算コストのかかる楕円型方程式を解く必要のない準圧縮系 [1] とする. 準圧縮系は, 音速を基本場での値で代換えすることで 完全圧縮系に比べて計算コストの増大を少なくした近似方程式系 であり, 地球大気の雲対流モデルにおける今日の標準的な枠組みの一つとなっている [8]. 本研究では, このような準圧縮系の木星大気の雲対流への応用可能性を探ることが目的である. 以下 第 2 節では, 開発した雲対流モデルの定式化と離散化の概要, および 3 種類の凝結性成分の雲を表示するための可視化方法について解説する. 第 3 節 では開発したモデルを用いた計算の例として, 対流圏界面付近の放射冷却と惑星内部からの熱輸送を模した熱的強制を与えた雲対流の長時間数値計算の結果を示す. 第 4 節ではまとめを行う.

図 1.1: 鉛直 1 次元熱平衡大気モデルによって求められた 木星大気中の雲の鉛直分布. 凝結成分元素の水素に対する存在比を太陽での値 [9] と同じとした. 高度は静水圧平衡の式より求めたものであり, 30 bar 面高度を高度 0 km としている. この計算は Sugiyama et al. (2006) [7] によって開発された計算コードを用いた [10].
| 木星大気の雲対流の直接数値計算 | << Prev | Index| Next >> |