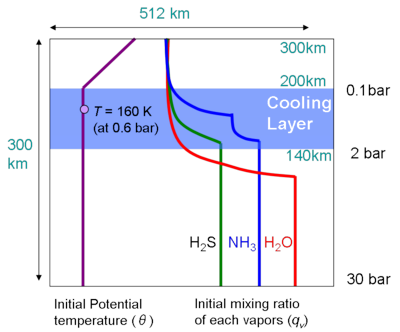
図 3.1: 系の設定の概要
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |
計算領域は鉛直方向に 300 km (下端の圧力は 30 bar, 上端の圧力は 0.001 bar), 水平方向は 512 km とする. 空間格子間隔は水平鉛直ともに 2 km とする.
モデル大気に対して, 対流圏界面付近の放射冷却と惑星内部からの熱輸送を模した熱的外部強制を与える. 対流圏界面付近の冷却強制は, ガリレオ探査機の放射観測 [14] で正味の冷却が観測された高度 2 bar (z = 140 km) から 0.1 bar (z = 200 km) の間に与える. 冷却の大きさは Nakajima etal. (2000) [6] と同様に -1 K/day とする. この値は現実の木星大気での値よりも 100 倍程度大きい. 大気深部からの加熱は, 下記の熱的境界条件として表現する.
水平境界には周期境界条件を適用する. 上部境界において, 応力なし, 鉛直速度なし, 温位フラックスなし, 凝結性成分気体の混合比フラックスなし, を仮定する. 下部境界においては, 応力なし, 鉛直速度なし, を仮定し, さらに大気深部の対流による速やかな熱と凝結成分気体の供給を念頭において, 下部境界での温位と凝結性成分気体の混合比は初期値に固定する. 下部境界における拡散係数の値は k = 800 m2s-1 に固定する.
初期の鉛直温度分布は 0.6 bar 面高度で 160 K とし, 下部境界から 200 km (p = 0.1 bar) までは断熱的, その上部は温度一定とする. 対流運動を発生させるための種として, 高度 110 km の各格子点に乱数的な微小温位擾乱を与える.
下部境界において, 凝結成分元素の水素に対する存在比を太陽での値 [9] と同じとする. それぞれの凝結成分混合比の鉛直分布は, 下部境界から凝結高度付近までは一定値とする. その高度より上では飽和に近い値を与えた. 詳細は 補遺 E を参照のこと.
数値積分は 106 秒 (約 300 時間) 行う. 数値積分終了時点では, 水平平均した大気構造は統計的には定常的となっている.

|
|
図 3.1: 系の設定の概要 |
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |