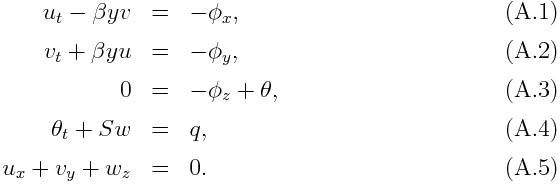
| Appendix A. Brief review of wave-CISK | [prev] [index] [next] |
For consideration of the atmospheric motion in the earth's tropics, the "equatorial beta plane" approximation, where the variation of metric is ignored and the Coriolis parameter is approximated to be proportional to latitude, is widely used. In this framework, the basic linearlized equations that describe the motion of three dimensional vertically stratified Bousinesq fluid are as follows:
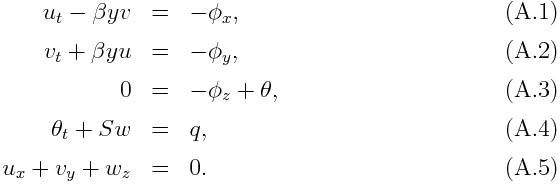
Here, (x, y, z) are northward, eastward, and vertically upward coodinates, respectively, denoting y=0 to be the equator, (u, v, w) are northward, eastward, and vertically upward components of wind velocity respectively, ¦µ is height field, ¦È is temperature field, S is vertical gradient of temperature of the basic field, and q is condensation heating. and subscripts represent partial derivative with respect to the variable.
In the formulation of wave-CISK by Hayashi(1970), condensation heating, q, is assumed to be
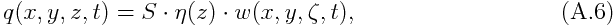
namely, the vertical structure of heating is separated from the temporal and horizontal structure, where ¦Æ is the height of the top of the mixed layer that is typically around 1 [km]. In this formulation of heating, a "scale separation" between cumulus activity and large-scale motions is assumed; the set of equations above describe large-scale motion, while cumulus activity is described only by "q". Cumulonimbi, the main heating agents in the conditionally unstable tropical atmosphere, are triggered by the low level upward motion and develop to the tropopause, heating the whole depth of the troposphere in their life time which is of the order of one hour; it is quite short compared with the time scale of the evolution of large-scale motions which is of the order of days.
We do not dwell on the issue of the adequacy of this assumption here, although there are actually a large number of arguments. One important notice to be added here is about the relationship with the Kuo scheme. In the calculation of heating in the Kuo scheme that is used in this study, the total amount of heating is proportional to the low level moisture convergence, which is approximately proportional to the low level upward motion. The vertical profile of heating is determined by the temperature structure of the atmosphere, which means that, considering the temperature structure in the tropics is horizontally nearly uniform, the vertical profile of heating can be actually almost independent of horizontal position and time. This assures that the structure of heating calculated with the Kuo scheme is similar to that represented by the simple formula above.
Assuming that the variables are periodic longitudinally and temporally, we can represent them as proportinal to
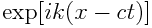
we can separate vertical and latitudinal dependence of variables, also. The zonal phase velocity, c, is allowed to take a complex value. If the imaginary part is positive, the disturbance grows exponentially. Assuming that
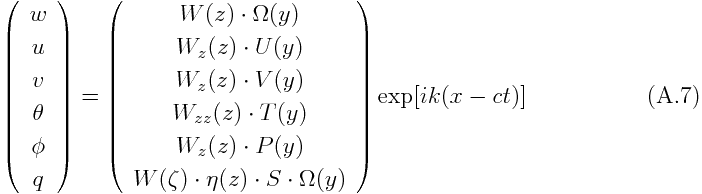
and, after some rearrangiment of equations, we obtain the vertical structure equation for W(z), which is
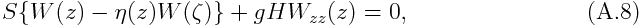
and the horizontal structure equations for U(y),V(y),P(y), which are
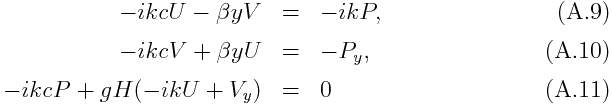
where the separation constant, H, is called "equivalent depth". The accerelation of gravity, g, is introduced so that H has a dimension of length and the horizontal structure equations become the same as the shallow water equations on the equatorial beta plane examined by Matsuno (1966).
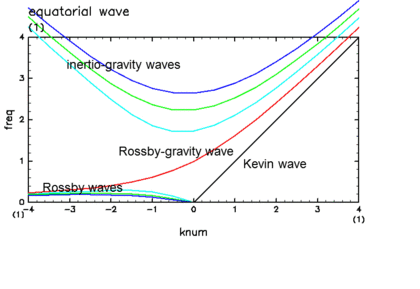
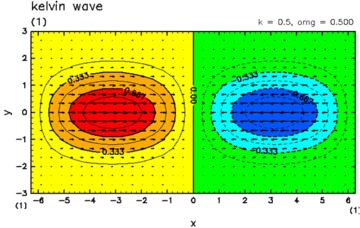
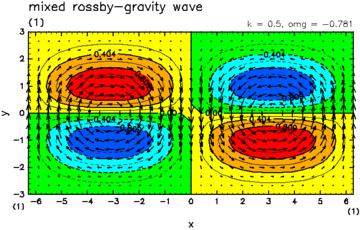
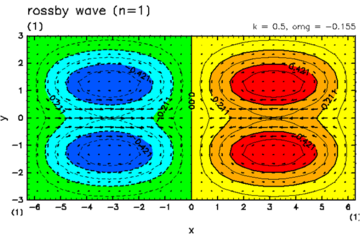
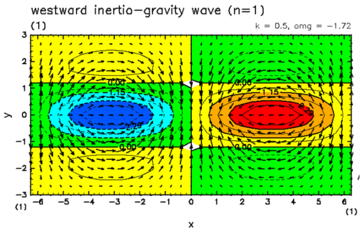
If there is no condensation heating (¦Ç=0), and hence H is positive real number, then, there are one eastward propagating Kevin wave, one Rossby-gravity wave, countably infinite set of Rossby waves, and, countably infinite set of inertio-gravity waves as the eigen modes which have amplitude around the equator and vanish at infinite y (Matsuno, 1966). The dispersion relations of those modes and the horizontal structures of some important ones are shown in Fig.A.1, and Fig.A.2, respectively.
|
| Fig.A.1: Dispersion relations of equatorial waves. Plotted are frequency (vetical axis) agains wavenumber (horizontal axis). |
|
|
|
|
| Fig.A.2: Horizontal structures of equatorial waves. (upper left) Kelvin wave, (upper right) Mixed gravity wave, (lower left) Rossby wave, (lower right) gravity wave. | |
Among these modes, Kelvin wave is the most directly related to the present study. Kelvin wave has the largest amplitudes of U, V, and P at the equator, and its phase velocity is independent of wavenumber (i.e., non dispersive), the value of which is related to the equivalent depth as

Now let us return to the problem of equatorial wave-CISK. The vertical structure of heating, ¦Ç(z), is assumed to be given. And then the vertical structure equation can be solved as an eigen value problem with appropriate vertical boundary condition, and one can obtain a set of vertical modes and corresponding equivalent depths (the separation constant) as eigen values. By substituting one of equivalent depths into the horizontal structure equations, one can obtain the dispersion relation and the horizontal structure of various horizontal modes. Therefore, the existence or absence of unstable modes can be discriminated by the existence of complex equivalent depth in the vertical structure equation. It should be noted that all of the modes of horizontal structure equation will be unstable if the equivalent depth is complex.
The condition for the appearance of complex equivalent depth will be discussed in the next subsection. Here, summarizing the result, complex equivalent depth and thus unstable modes, appear when the heating by cumulus clouds, i.e. ¦Ç, is strong in the upper troposphere.
When the instability is not extremely strong, i.e., the absolute value of the imaginary part of the equivalent depth is fairly smaller than that of the real part, the horizontal structure of the unstable modes are similar to those given by the shallow water equations with the realpart of the equivalent depth; for a particular complex value of equivalent depth, there are Kelvin, mixed Rossby gravity, Rossby, and inertio gravity waves, and the number of them, their dispersion relation (Fig.A.3), and north-south structure of each type of modes are similar to those in the shallow water equation. One of the important difference is that phase tilts exist in north-south direction, as well as vertically.
When the equivalent depth is complex, the corresponding vertical mode is a complex function of height. This means that the phase shifts in east-west direction or in time as the height varies. Typically, the phase line of an unstable mode of wave-CISK delays to the west as the height increases, so that the unstable Kelvin mode propagating eastward along the equator have a westward phase tilt in height (Fig.A.5).
| [prev] [index] [next] |