Appendix A.2 Mechanism of emergence of propagating growing mode

In the followings, we will briefly describe dependence of the appearance of complex phase speed on condensation heating parameter, and the mathematical structure of the mode solutions in the system given in subsection A.1.

Reduced gravity effect and CIFK

As the simplest set-up, we assume that the vertical velocity vanishes at the ground surface (z=0) and the tropopause (z=D). Without heating, the vertical structure equation (A.8) is

has eigen modes and the corresponding eigen functions represented by

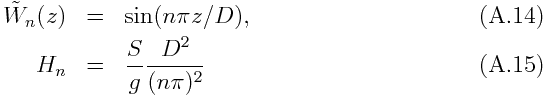
This indicate, for instance, the eastward propagation velocity of Kelvin wave (A.12) is smaller for the larger mode index (vertical wavenumber) n.

Before examining the wave-CISK in detail, we will check the properties of CIFK. In clouds, water vapor condenses and release the latent heat. This process can be represented by assuming that heating occurs directly proportional to the vertical motion at the same height like

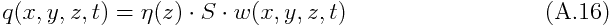
Note the difference from (A.6), i.e., the vertical position of the vertical motion adopted. The signature of η is usually positive. This modifies the vertical structure equation (A.8) into

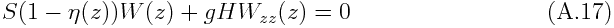
In the simplest case where η is a positive constant, the static stability, S, in the vertical structure equation without heating can be thought to be replaced by the effective static stability

In this case, the vertical structure of eigen modes do not change from those in the no heating case (A.14), but the eigen values change. Replacing S in (A.15), since η is positive, the equivalent depth and therefore the phase velocity of Kelvin wave become smaller. This effect of condensation heating is called as "reduced gravity" or "reduced stability" effect (Gill, 1982).

If heating is strong enough, so that η exceeds 1, (A.18) indicates that Seff becomes negative, and from (A.15) equivalent depth becomes also negative. In this case, in the horizontal structure equations, the phase speed of each mode becomes pure imaginary, which indicates the existence of stationary growing disturbances. These unstable modes are basically the same as those of convective instability in a non-rotating system in the sense that effective stability, Seff, is negative. The growth rate is the larger for the smaller horizontal scale mode. (For smaller horizontal scale disturbances, the hydrostatic relation assumed in (A.3) breaks down. However, if the vertical acceleration term is kept in (A.3), the growth rate at the infinitesimal horizontal scale remains finite.) In the atmosphere, the situation where the vertical temperature gradient exceeds the moist adiabatic lapse rate can be considered as a case where η is grater than 1. The instability caused by the heating proportional to in situ vertical velocity can be regarded as a model of CIFK. Stationary growing disturbances can be, in this sense, referred to as CIFK solutions.

Emergence of propagating unstable modes due to interaction between vertical modes

The vertical structure equation of wave-CISK (A.8) can be solved, after discretization, for example by a finite difference method, as a matrix eigen value problem. When η is small in the lower levels and is large in the upper levels, actual calculation can show that there are cases where complex (non-zero real and imaginary parts) equivalent depth can be obtained (Fig.A.3). This indicate that there are propagating growing modes for such cases. The existence of propagating growing modes is the reason of calling the instability as "wave"-CISK. It is noted that the vertical profile of heating, η, preferable for the emergence of the propagating unstable modes is, as the sum of condensation and eddy heat transport, similar to that of cumulonimbi in the tropics.

Fig.A.3: Example of dispersion relation for equatorial wave-CISK. Complex phase speed (vertical axis) against wavenumber (horizontal axis). (left) real part, (right) imaginary part. Four layers are adopted as vertical discretization.

The reason why complex equivalent depth emerges in wave-CISK formulation is unclear in the present stage. However, when the vertical structure equation is expanded using the system of eigen modes of the heating-free vertical structure equation, we can understand the mathematical structure behind to some extent. In the followings, we are going to present a summary of the arguments by, for instance, Lau and Peng (1987), Chang and Lim, (1988), Numaguti and Hayashi (1991) and so on.

If we expand vertical velocity and heating as

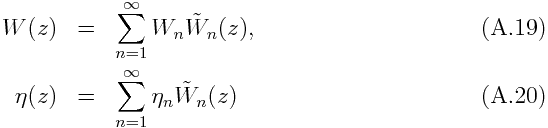
and substitute them in the vertical structure equation (A.8), we obtain

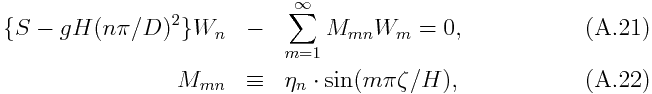
where Mmn represents interaction coefficient between the vertical modes induced by heating; diagonal elements represent self-feedbacks, and off-diagonal components represent interaction between different modes.

When Mmn is a diagonal matrix, the independence of modes is preserved, but equivalent depth of each mode changes from the non-heating case due to the modification of effective static stability resulting from self-interaction. v The important point is that, since the signature of Mmn is determined by the profile of condensation heating, equivalent depth is not necessarily decreased (reduced gravity effect); in some profiles equivalent depth is increased (enhanced gravity effect).

As the simplest example of wave-CISK, let us consider the case where the heating profile is represented as the sum of only the first and the second vertical modes. Then, only the first and the second modes interact, and the self-contained system of equations can be extracted from the vertical structure equation as

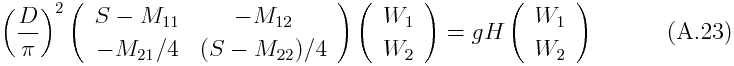
The condition for H to be complex is that the discriminant becomes negative.

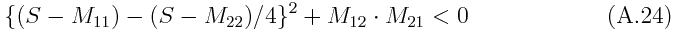
When the heating is weak in the lower levels and strong in the upper levels, its projection on the first mode, η1, is positive and that of the second mode, η2, is negative. And hence the coefficients of the interaction will be

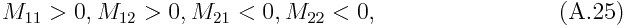
Since the second term of the discriminant (A.24) is negative, if the first term is sufficiently small, equivalent depth becomes complex. It may be more comprehensible if we present a direct expression of eigen values and an argument about the change of phase speeds.

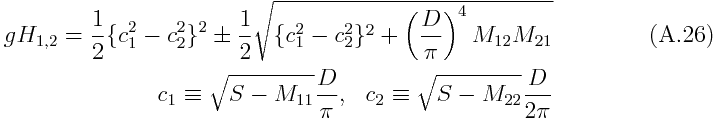
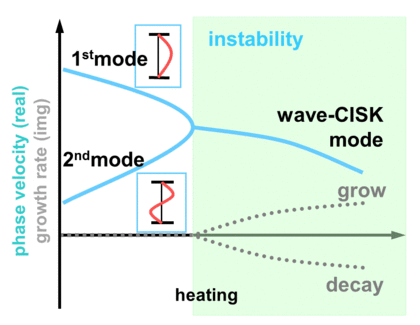
where double sign indicates that positive for the first mode, and negative for the second mode, and c1 and c2 are the "pure" phase velocities for each mode with only the effect of self-interaction is considered, respectively. When there is no condensation heating (η1=η2=0), the phase speed of the first vertical mode is larger than the phase speed of the second vertical mode. When condensation heating is introduced, since M11 is positive, reduced gravity effect occurs for the first vertical mode. Equivalent depth and therefore the phase speed of the first mode decreases as the increase of η1. As for the second vertical mode, since M22 is negative, enhanced gravity effect occurs. Equivalent depth and therefore the phase speed of the second mode increases as the increase of |η2|. As the increase of condensation heating, the difference between the phase speeds of the two modes reduces, and eventually complex equivalent depth appears (Fig.A.4).

Fig.A.4: Relationship between condensation heating and interaction of vertical modes.

Vertical structure of the unstable mode

When equivalent depth is complex, the expansion coefficients of the first and second modes is also complex. This means that both modes are superposed with some difference of phase; equivalently, a temporal or longitudinal phase shift exists for different altitudes. Fig.A.5 shows veridical structures corresponding to Kelvin wave modes. There is no phase shift in the vertical direction for neutral first or second modes (upper panels of Fig.A.5). For wave-CISK mode (lower panel of Fig.A.5), westward phase shift as the increase of altitude can be seen.

Fig.A.5: Vertical structures corresponding to Kelvin wave modes. (upper left panel) neutral (no condensation heating) first mode, (upper right panel) neutral (no condensation heating) second mode, (lower panel) wave-CISK (with condensation heating) mode.