3.2 その他細部
具体的な計算手順は、基本的にDritschel(1989)に従う。
< ノードの再分配 >
ノードは、最初は規則的な間隔で配置されているが、 時間が経過すると不均一な間隔になる。 ノードの分布が不均一になると速度場の計算に大きな誤差が生じる。 また不必要に過密な分布は計算時間の増大を招く。
そこで計算途中でノードを適切に再分配する必要がある。
具体的には、まずノード xi での曲率κi
を 前後3点 xi -1 , xi
, xi +1 を通る円の曲率とし、ノード密度ρi
という量を定める。
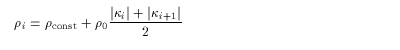(3.4)
xi -1 , xi , xi
+1 のつくる角度が90度以下の点をコーナーとして固定し、
あるコーナーから次のコーナーまでのコンターセグメントごとに
ノードを再分配する(コーナーがない場合は、先頭のノードを固定する)。
新しいノード数 n ' は、ρi
を用いて
(3.5)
で定める([ ]はガウス記号)。
そして、次式をみたすような i , p
をさがす。
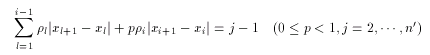(3.6)
新しいノード xj の位置は、 古いノード
xi , xi +1
の間 の x ( p ) となる。 ただし x
( p ) は3次スプライン補間によって求める。
< 補間 >
となりあうノード xi , xi
+1 間の 補間は、3次スプライン関数を使用する。
(3.7)
ただし、
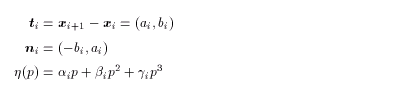(3.8)
である。補間係数 αi ,βi ,γi
は、 曲率 κi を用いて
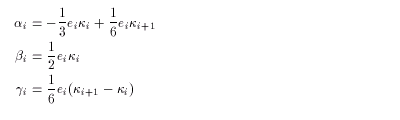(3.9)
で与えられる。ここで、κi と ei
は
(3.10)
である。つまりこの補間では、xi , xi
+1 において x および κi
が連続であると仮定して係数を決めている。