Appendix C: 数値モデルの基礎方程式

以下、数値モデルの概要を簡略に述べる (技術的な詳細は中島(1994)を参照)。

力学的な枠組は、非弾性方程式系 (Ogura and Phillips, 1962) を用いる。

鉛直・水平成分の運動方程式は、

$\displaystyle\DD{u}{t}$	$\textstyle=$	$\displaystyle-c_{p}\Theta_{0}\DP{\pi}{x} + D(u),$	(16)
$\displaystyle\DD{w}{t}$	$\textstyle=$	$\displaystyle-c_{p}\Theta_{0}\DP{\pi}{z} + b + D(w).$	(17)

ここで、各式左辺の $\DD{}{t}$ はラグランジュ的時間微分

$\begin{displaymath} \DD{}{t} \equiv \DP{}{t} + u \DP{}{x} + w \DP{}{z}\end{displaymath}$

(18)

である。また右辺の D は乱流混合の寄与であり、混合される物理量を Y と書いて、

$\begin{displaymath} D_{}(Y) \equiv \DP{}{x}(K\DP{Y}{x}) + \Dinv{\rho_{0}}\DP{}{z}(\rho_{0} K\DP{Y}{z})\end{displaymath}$

(19)

により計算する。但し、K は乱流混合係数であり、 Klemp and Wilmhelmson(1978) にならい、風速場の変形速度と局所的な鉛直安定度に基づき prognostic に計算する。

また ( 17 ) 右辺の b は浮力の項

$\begin{displaymath} b_{} \equiv g ( \frac{\theta}{\Theta_{0}} + (\frac{m_{n}}{m_{v}}-1) q_{v} - q_{c} - q_{r} )\end{displaymath}$

(20)

である。また、u と w には連続の式

$\begin{displaymath} \DP{(\rho_{0}u)}{x} + \DP{(\rho_{0}w)}{z} = 0 \end{displaymath}$

(21)

を満たすことを要請する。これにより、無次元圧力関数 $\pi$ が診断的に定まる。

熱力学第一法則は、

$\begin{displaymath} \DD{\theta}{t} + w\DP{\Theta_{0}}{z} = \frac{L}{c_{p}\Pi_{0}}( C - E_{r} ) + D(\theta) +D(\Theta_{0}) + Q_{rad}\end{displaymath}$

(22)

である。ここで C は水蒸気の凝結、E_r は雨水の蒸発であり、また、Q_rad は放射過程の寄与を簡単化して表現した body cooling である。

水物質としては、気相（水蒸気）と液相のみを扱う。さらに液相を、雨水・雲水に分け、雨水については周囲の空気に対しての落下を考慮する。すなわち、雲微物理過程についてはバルクパラメタリゼーションを行なう。これら水物質の保存の式は、

$\displaystyle\DD{q_{v}}{t}$	$\textstyle=$	$\displaystyle- C + E_{r} + D(q_{v}),$	(23)
$\displaystyle\DD{q_{c}}{t}$	$\textstyle=$	$\displaystyleC - P_{rc} + D{q_{c}},$	(24)
$\displaystyle\DD{q_{r}}{t}$	$\textstyle=$	$\displaystyle+ P_{rc} - E_{r} - \Dinv{\rho_{0}} \DP{}{z}(\rho_{0}V_{T}q_{r}) + D(q_{r}).$	(25)

である。

運動学的境界条件として、領域の上端と下端で鉛直流がゼロであることを要請する。また、水平方向には全ての変数について周期的であることを要請する。

雲微物理過程は、基本的に Kessler(1969) のバルクパラメタリゼーションに従う。

雲水は粒の大きさが小さく、従って、水蒸気との間で瞬間的に saturation adjustment が起こるとする。即ち、移流などの項を計算した後の温度と水蒸気量が過飽和状態となっている場合には、ちょうど飽和になる量の水蒸気を凝結させる。一方同様に移流などの計算を行なった後、雲水が存在するにも拘らず未飽和となっている箇所では、ちょうど飽和となるまで雲水を蒸発させる。もし、それに必要な雲水が無ければ、全ての雲水を蒸発させる。以上の過程で、当然、凝結の潜熱の出入りを計算に入れる。

雲粒は、まずその相互の衝突により粒径を増し、雨粒を生成する。この過程を autoconvsersion とよぶ。雨粒が生成した後は、雨粒は落下しつつ雲粒を捕獲して成長する事ができる。水物質の保存の式の中の P_rc は、この二つの寄与の和である。

P_rc = P_autoconv + P_collect

(26)

autoconversion の項は、雲微物理のバルクパラメタリゼーションの中でも議論の多い部分であるが、ここでは、Berry(1968) に従って

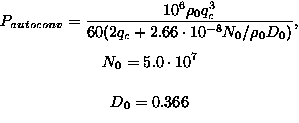$\begin{displaymath} P_{autoconv} = \frac { 10^{6} \rho_{0} q_{c}^{3} } {60 ( 2 ... ..._{0} D_{0} ) }, \ N_{0} = 5.0 \cdot 10^{7}, \ D_{0} = 0.366\end{displaymath}$

(27)

により計算する。

雨粒は、常に指数型の粒径分布 (Marshall and Palmer, 1948 )をしていると仮定する。バルクの落下速度・雨による雲粒の捕獲・雨の蒸発は、この仮定のもとで、それぞれ、

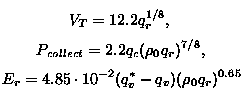$\begin{displaymath} V_{T} = 12.2 q_{r}^{1/8}, \ P_{collect} = 2.2 q_{c} ( \rho... ...ot 10^{-2} ( q_{v}^{\ast} - q_{v} ) ( \rho_{0} q_{r} )^{0.65}\end{displaymath}$

(28)

により計算する。

数値モデルの基礎方程式

Kensuke Nakajima
1/31/1998