| 二つの渦輪の干渉 |
二つの渦輪の干渉を解析することは渦の繋ぎ換えという流体現象の素過程を調べる上で重要である。 計算の場合は主として,渦度,渦線そのものを表示することにより解析が行われる。 一方,可視化実験の場合は,渦輪を構成するトレーサー粒子の動きを見ることになる。 実験との比較を考えた場合は計算の方で実験と同等の可視化を行う方が簡単である。 この目的に対し受動的スカラー量の可視化が考えられるが,計算をオイラー的に行うと一般的には数値拡散が強い解となり,実験での可視化とは異なる結果となってしまう。 そこで,仮想粒子追跡を行うのだが,粒子分布だけで特徴領域を表現することは難しい。 また,実験との比較を意識した場合,粒子追跡の際に前節で示したトレーサー粒子の拡散効果を考慮した方が妥当な結果となる。 これは対流効果だけでは粒子群のパターンに初期依存性が現れるためでもある。 但し,今回の数値実験では拡散効果の差異は見掛け上小さなものであった。 定量的な差がどの程度あるのか, また,粒子密度を計算する際の数値的な拡散についての検討は今後の課題として残る。
拡散効果を加味した粒子追跡法による粒子分布から求めた粒子密度の時間変化を図12に示す。 粒子濃度の高い部分の形成過程が仮想粒子密度の可視化から明確に捉えられており,渦の繋ぎ換えという現象をラグランジェ的に解釈する上で役立つものと思われる。
図12 二つの渦輪の干渉 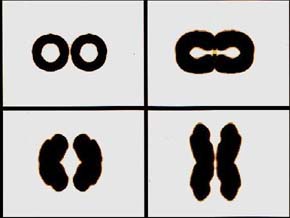
![]()