Introduction (2) - our purpose

In this study, we will investigate the influence of the thermal boundary condition on two-dimensional convection in a rapidly rotating cylindrical annulus where the top and bottom boundaries in the direction of the rotation axis are inclined against the rotation axis causing the topographic b effect.

The geometry is designed as a conceptual model of thermal convection in a rapidly rotating spherical shell. Based on the Taylor-Proudman theorem, fluid motion is expected to be uniform in the direction of the rotation axis when the rotation rate is large. The rotation of the system affects the two-dimensional convective motion only through inclination of the boundaries. The most important difference between the configuration of the present system and that of Dowling (1988) is the direction of the gravity axis; In our model it is perpendicular to the rotation axis while it is parallel in Dowling's (1988).

As for the fixed temperature boundary condition, convection in the present geometrical configuration was examined by Busse (1986) with the linear and weak nonlinear theories, and by Busse and Or (1986) with numerical calculations. Behavior of the convection in high Rayleigh numbers was examined by Brummell and Hart (1993) with numerical calculations. They showed that the horizontal scale of convection cells becomes smaller as the rotation rate increases. The effect of rotation on the horizontal size of convection cells is expected to compete with the possible effect of fixed heat flux boundary condition also in the case of convection in a rotating cylindrical annulus with inclined top and bottom boundaries.

Study on rotating thermal convection under a fixed heat flux boundary condition is important for understanding fluid motions in the core of the earth and planets. The fixed heat flux boundary condition is an extreme situation of a fluid in contact with a boundary with small heat conductivity. This fixed temperature boundary condition implies that the boundary material has infinite heat conductivity, while in reality, the earth's mantle has smaller heat conductivity than the fluid core.

In the following sections we describe model configurations and governing equations, and perform a linear stability analysis. Time developments of thermal convection are presented by nonlinear numerical computations. The final sections include the physical interpretations and discussions.

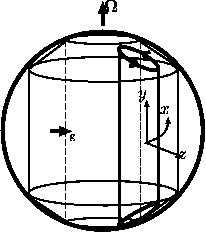Fig.2 Schematic picture of the system