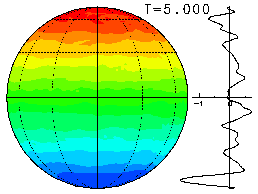3.1 Overview of the Time Evolution of the Vorticity Field and the Zonal-Mean Zonal Flow
3.2 Generation of easterly polar vortex
3.3 The Condition Required for the Appearance of the Band Structure

3.1 Overview of the Time Evolution of the Vorticity Field and the Zonal-Mean Zonal Flow

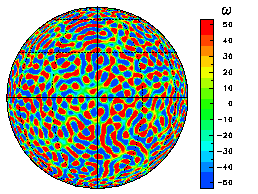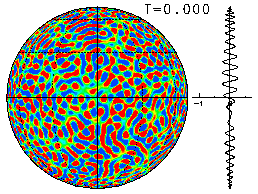
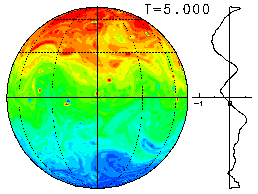
We present an overview of the time evolution of the flow field in real space by showing the changes of the vorticity field and the zonal-mean zonal flow. The figure on the right shows (one example of) the initial value as a field of vorticity ω.

The initial parameters are n₀ = 50 and γ = 1000, and the truncation wavenumber is T341.

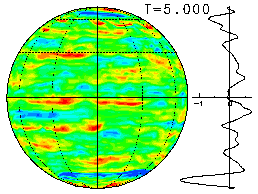
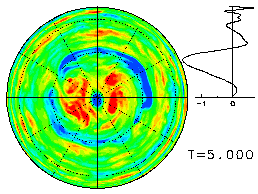
Here, the colors red and blue denote areas of positive and negative vorticity, respectively. In addition, the zonal-mean angular momentum (u cosφ) is shown to the right of the plot.

The visual representation of the vorticity field is an orthographic projection(equatorial aspect) and the latitude and longitude are drawn for every 30 degrees.

The time evolutions for three values of Ω (=0, 50, 400) started from the same initial values are shown below. The plots below show the final state for each value of Ω. Click on the plots to view the animation of the time evolution from the initial state.

Since the figures below show the field of absolute vorticity q = ω + 2Ωμ, please note that the effect of planetary vorticity (2Ωμ) adds the NS gradient to the relative vorticity field when Ω ≠ 0.

In the case of Ω = 0

In the case of Ω = 50

In the case of Ω = 400

• When Ω =0, coherent vortices are formed, as in the results of numerical experiments on a planar domain by McWilliams(1984), and interactions such as the merger of vortices are observable.
• In the cases of Ω =50 and 400, the vortex merger process are observed as in the case for Ω = 0. However, the gradient attributed to planetary vorticity (2Ωμ) makes Rossby waves, which is seen as fluctuations of the contour lines for q, dominant in the mid-to-low latitude regions.
• In the case of Ω = 400, banded structures of zonal flows are observed in the mid-to-low latitude regions, and easterlies are predominant at high latitudes. (In this example, this effect is especially prominent near the South pole.)

Since the above figures plot the fields of absolute vorticity q, the fine structures of the vorticity field are difficult to discern due to the gradient attributed to planetary vorticity for Ω = 400. Thus, we will show the time evolution only for the relative vorticity ω below.

In addition, a plot showing the prominent easterly polar vortex around the South pole has also been made.

In the case of Ω = 400 (relative vorticity)

In the case of Ω = 400 (relative vorticity: viewed from over the south pole)

• It can be seen that the vorticity field also displays structures elongated in the zonal direction as the band structure of zonal flow in mid-to-low latitudes and bands of positive/negative vorticity become aligned parallel from the north to south.
• When viewed from over the South pole, it can be seen that the areas having positive relative vorticity become concentrated around the pole with the appearance of the easterly polar vortex. In other words, with respect to absolute vorticity, the latitudinal gradient has become small near the South pole.

<<index <previous next>