A Boussinesq fluid is governed by
the equations of heat, motion and continuity (e.g. Kimura, 1983):
where, T is temperature,
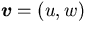 is velocity,
is velocity,
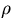 is density, P is pressure,
is density, P is pressure,
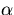 is the thermal expansion coefficient,
is the thermal expansion coefficient,
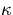 is thermal diffusivity,
is thermal diffusivity,
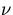 is kinematic viscosity,
is kinematic viscosity,
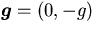 is acceleration of gravity.
is acceleration of gravity.
We introduce the stream function
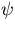
as
|
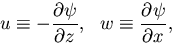 |
(17) |
Subsituting this into (14) and
(15), we obtain
| | |
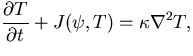 |
(18) |
| | |
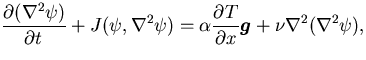 |
(19) |
where J(A,B) is the Jacobian
|
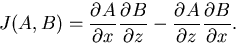 |
(20) |
The governing equations are non-dimensionalized
using the thickness of the fluid layer
b as the length scale,
the thermal diffusion time
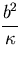 as the time scale,
and the temperature difference between the boundaries
as the time scale,
and the temperature difference between the boundaries
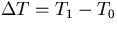 as the temperature scale,
yielding,
as the temperature scale,
yielding,
Here
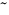 denotes a non-dimensional variable.
Equations (18) and
(19) then become
denotes a non-dimensional variable.
Equations (18) and
(19) then become
| | |
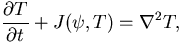 |
(21) |
| | |
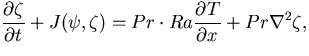 |
(22) |
where,
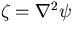 is vorticity,
is vorticity,
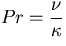 is the Prandtl number, and
is the Prandtl number, and
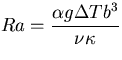 is the Rayleigh number.
The subscirpts
is the Rayleigh number.
The subscirpts
 denoting a non-dimensional variable
are omitted for simplicity.
denoting a non-dimensional variable
are omitted for simplicity.
A fixed temperature condition is specified
at the top and the bottom boundaries:
|
 |
(23) |
The kinematic and dynamic boundary conditions are impermeable,
and free-slip, such that
|
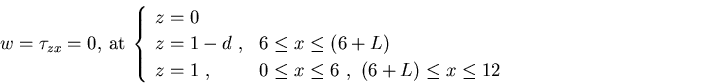 |
(24) |
|
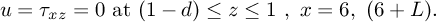 |
(25) |
Horizontal boundaries are periodic.
These kinematic and dynamic conditions are described by
the voriticity and the stream function.
The impermeable condition becomes
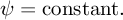 |
| |
(26) |
Since the initial condtion is one of no motion and
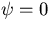 ,
stream function always vanishes at the boundaries,
,
stream function always vanishes at the boundaries,
|
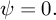 |
(27) |
Since w=0 at the horizontal plane of the boundaries,
the free-slip condition becomes
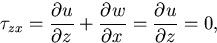
that is,
|
![\DP[2]{\psi}{z}=0.](img70e.gif) |
(28) |
Further, since
![\DP[2]{\psi}{x}=0,](img71.gif)
at the horizontal plane of the boundaries,
we have,
|
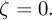 |
(29) |
By following the similar procedure for vertical plane of the boundaries,
we obtain (29).
is velocity,
is density, P is pressure,
is the thermal expansion coefficient,
is thermal diffusivity,
is kinematic viscosity,
is acceleration of gravity.
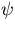
as the time scale, and the temperature difference between the boundaries
as the temperature scale, yielding,
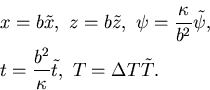
denotes a non-dimensional variable. Equations (18) and (19) then become
is vorticity,
is the Prandtl number, and
is the Rayleigh number. The subscirpts
denoting a non-dimensional variable are omitted for simplicity.
, stream function always vanishes at the boundaries,