Numerical calculations (3) -the case of a plate covering the whole surface The horizontal cell sizes of mantle convection induced by the effect of continental plates Numerical calculations (2) -horizontal cell sizes of convection cells The boundary-layer theory (1) -convection beneath the plate
 
Figure 5: Comparison of convection patterns for (a) the case of no plate (L=0) and (b) the case in which a plate covers the whole surface (L=6). The computational domain is 6x1. Ra=105, Pr=10, and d=0.1. The cases for Ra=104 and Ra=106 are presented in Appendix B.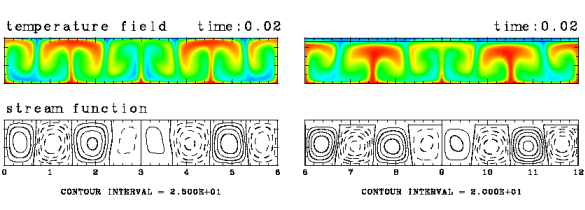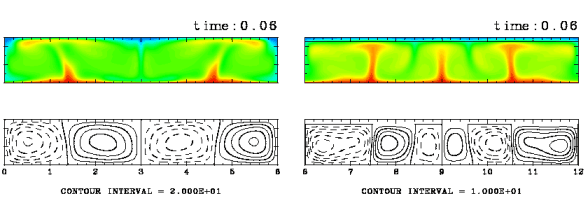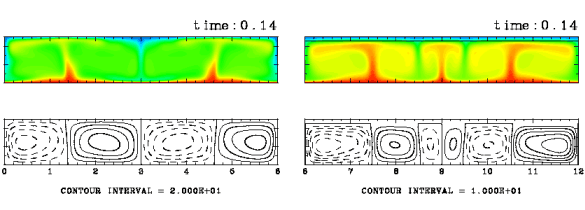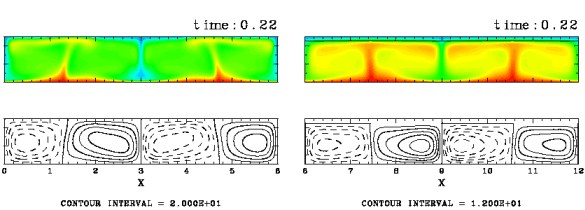

pl06ra5.gif (9118 bytes)

It is anticipated that the emergence of upwellings beneath the plate are caused by the thermal effects of the plate”Ēs presence. The fluid under the plate is presumed to be warmed, since it is hard to transport heat to the surface. In order to investigate and confirm such an effect, we have performed further experiments in which the upper surface is completely covered with a plate, and compared the results with those for the case of no plate.

The left panel of the above figure shows the case without a plate, and the right shows the case where a plate extends over the whole surface. We observe that irrespective of the assumed Rayleigh number, the fluid temperature beneath the plate is higher than when no plate is present. The vertical distributions of horizontally average temperature reveal that heat flux at the surface of the plate is lower than that at the surface without a plate. Thus, the heat flux is decreased by the existence of the plate.

tprofile.gif (1009 bytes)

Figure 6: The vertical distributions of horizontally averaged temperature. The red dotted and blue solid lines represent cases with and without a plate, respectively.

From this figure, we can summarize the characteristics of convection under the plate. A thermal boundary-layer is established beneath the plate, and the averaged temperature under the plate has a value between those of the temperatures at the lower boundary (1), and the fluid-plate boundary Tp. That is, the convection regime under the plate is similar to that without a plate except for the following points:

In the following section we estimate the temperature difference between the two cases by considering these two points in relation to ordinary boundary-layer theory.
Numerical calculations (3) -the case where a plate covers the whole surface Numerical calculations (2) -horizontal cell sizes of convection cells Numerical calculations (2) -horizontal cell sizes of convection cells The boundary-layer theory (1) -convection beneath the plate