The boundary-layer theory (2) -temperature beneath the plate

The boundary-layer theory (2) -temperature beneath the plate

In light of the schematic picture above, we define the temperature at the bottom of the plate to be T_p, the temperature of the fluid below the plate to be T_cp, and the temperature of the internal fluid outside the plate to be T_c. Since the temperature of the fluid below the plate T_cp is specified by

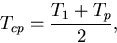$T_{cp}=\frac{T_{1}+T_{p}}{2}$ (5)

it is sufficient to evaluate T_p in order to obtain T_cp.
Using boundary-layer theory (Turcotte and Schubert 1982), the relation between the Nusselt number and the Rayleigh number is given by

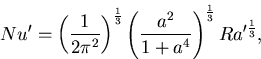$Nu' = \left(\Dinv{2 \pi^{2}}\right)^{\Dinv{3}}\left(\frac{a^{2}}{1+a^{4}}\right)^{\Dinv{3}} Ra'^{\Dinv{3}},$ (6)

where the prime denotes values for the convection under the plate, and a is the horizontal size of a convection cell. Since temperature and its gradient must be continuous at the boundary, we have

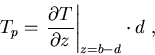$T_{p} = \left. \DP{T}{z}\right\vert _{z=b-d} \cdot d$ (7)

For the fluid beneath the plate, the thickness of the layer is 1-d and temperature at the top of the fluid layer is the temperature just beneath the plate T_p, Ra' is expressed in terms of the Rayleigh number for the whole layer Ra as,

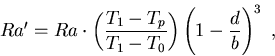$Ra' = Ra \cdot \left( \frac{T_{1}-T_{p}}{T_{1}-T_{0}}\right) \left( 1-\frac{d}{b} \right) ^{3} \$ (8)

From these equations, a relation between the temperature under the plate T_p and the Rayleigh number Ra can be straightforwardly obtained.

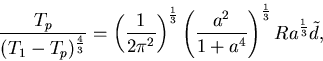$\frac{T_{p}}{(T_{1}-T_{p})^{\frac{4}{3}}} = \left(\Dinv{2 ...{a^{2}}{1+a^{4}}\right)^{\Dinv{3}}Ra^{\Dinv{3}} \tilde{d},$ (9)

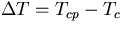From (9), T_p can be calculated for a given value of the Rayleigh number. Further, the averaged temperature of the fluid under the plate T_cp = (T₁+T_p)/2 and temperature difference induced by the plate $\Delta T = T_{cp}-T_{c}$ can also be estimated.

The boundary-layer theory (2) -temperature beneath the plate