| 数値計算 (3) -全表面がプレートの場合 |
 |
 |
 |
| 数値計算 (3) -全表面がプレートの場合 |
|
|
|
図 : プレートが存在しない場合と, 表面全体にプレートが存在する場合での対流の様子の比較. 領域は 6x1, Ra=105, Pr=10, d=0.1 の場合. (a) プレートが存在しない場合(L=0). (b) プレートが全表面に存在する場合(L=6).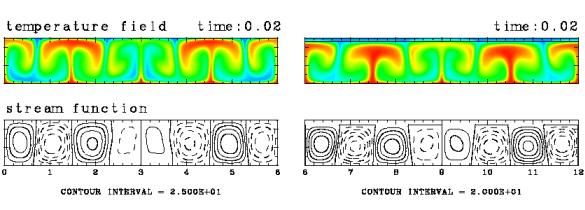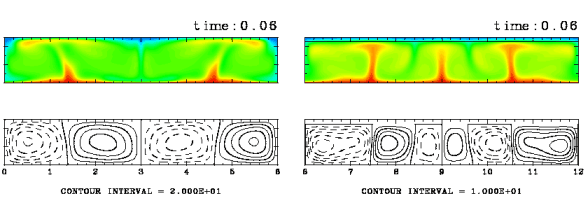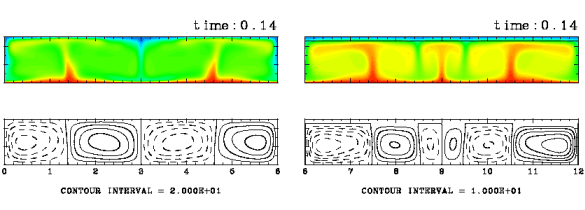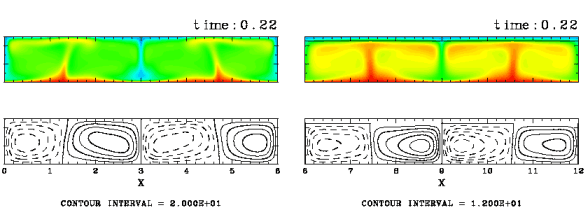 
|
プレートの下に上昇流が形成されやすいのは, プレートが熱を逃しにくいためにプレートの下の流体が 温められるからであると考えられる. そこで, プレートの存在によってどの程度下の流体が 温められているのか調べるために, 流体層表面全体をプレートで覆った場合と 全くプレートを置かない場合について それぞれ対流の計算を行ってみた. いずれの場合も流体層上部をプレートで覆った場合の方が プレートを置かない場合よりも流体が温められている. 鉛直温度分布に見られる表面での温度勾配に注目すると, プレート表面での熱流量が プレートのない表面のものよりも小さいことがわかる. つまりプレートによって熱が逃れにくくなっている. また, プレートで覆われた流体層の鉛直温度分布をみると, はじめプレート表面の熱流量よりも流体層下面からの熱流量の方が大きく, 時間とともに流体が温められて熱流量の収支がとられていく様子がみられる.
|
図 : 水平平均温度の比較. 実線(青)がプレートなし, 点線(赤)がプレートありの場合を表す. |
上図のプレート下の対流の水平平均温度分布には, プレートのない場合と同様に熱境界層が形成されており, 流体中心部の温度がプレートの底の温度と 流体層下面の温度の平均値となっている. したがってプレート下の対流の水平平均温度分布は, プレートが無い場合の対流と比較して,
と考えることができそうである. ただしTp はプレートの底での 温度である. そこで引き続く節において, プレートの影響によりプレート下の流体が どの程度温まるのかを, この特徴を足掛かりにして理論的に見積もってみる.
- 流体層の厚さが 1-d に変わった
- 上端の温度がプレートの厚さ分だけ温かくなった (
).
| 数値計算 (3) -全表面がプレートの場合 |
|
|
|
