境界層理論 (2) -プレート下の流体の温度

境界層理論 (2) -プレート下の流体の温度

先の水平平均温度構造の模式図のようにプレートの底の温度を T_p, プレートの下の流体内部温度を T_cp, プレートの外側での流体内部温度を T_c とする. 流体層内部温度は

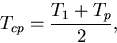$T_{cp}=\frac{T_{1}+T_{p}}{2}$ (5)

である. プレートの下の流体内部温度 T_cp を求めるにはプレートの底の温度 T_p がわかればよい.
プレートの下の流体層に対して境界層理論を応用すると (Turcotte and Schubert 1982),

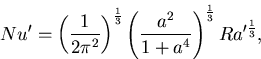$Nu' = \left(\Dinv{2 \pi^{2}}\right)^{\Dinv{3}}\left(\frac{a^{2}}{1+a^{4}}\right)^{\Dinv{3}} Ra'^{\Dinv{3}},$ (6)

となる. ここで, ' はプレートの下で定義されることをあらわしている. a は対流セルの水平スケールである. 境界面で温度と温度傾度が連続であることから

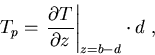$T_{p} = \left. \DP{T}{z}\right\vert _{z=b-d} \cdot d$ (7)

プレートの下ではプレートの厚さ分だけ流体層が薄く 1-d であり, かつ, 流体層の上面温度がプレートの底の温度 T_p であるので, レイリー数 Ra' は流体層全体のレイリー数 Ra を用いて

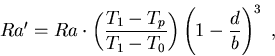$Ra' = Ra \cdot \left( \frac{T_{1}-T_{p}}{T_{1}-T_{0}}\right) \left( 1-\frac{d}{b} \right) ^{3} \$ (8)

と表される. これらを用いるとプレート下の温度 T_p とレイリー数 Ra の関係式が

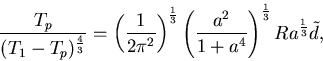$\frac{T_{p}}{(T_{1}-T_{p})^{\frac{4}{3}}} = \left(\Dinv{2 ...{a^{2}}{1+a^{4}}\right)^{\Dinv{3}}Ra^{\Dinv{3}} \tilde{d},$ (9)

とあらわされる. (9)より, レイリー数を与えればプレートの底の温度 T_p が求められる. さらには, プレート下の流体層内部温度 T_cp = (T₁+T_p)/2 とプレートの存在によって生じる理想的な状態での水平方向の温度差 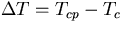$\Delta T = T_{cp}-T_{c}$ が求められる.

境界層理論 (2) -プレート下の流体の温度