3-3.  数値実験による安定性解析

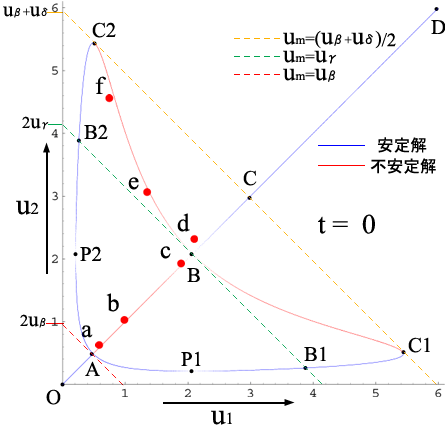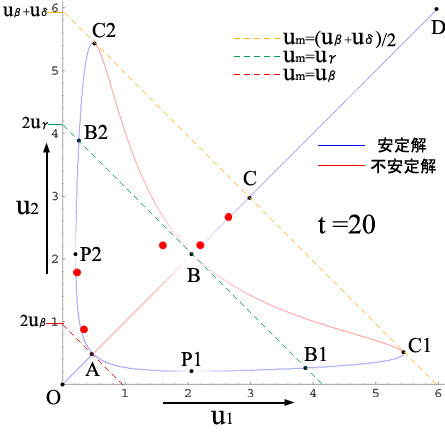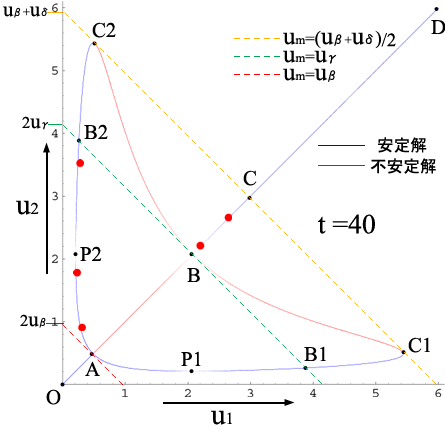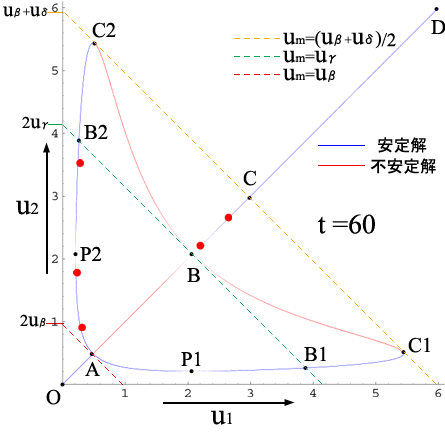
3-2で求められた状態は定常状態ではあるが，これだけでは安定な状態かどうかはわからない．定常解が複数あるの場合について数値実験(付5-1,2,3)で安定性を調べると，図7のようにAC1，AC2，BC1，BC2上の点で表される状態が安定で，AB，BC1，BC2上の点で表される状態が不安定であることがわかる．赤点a〜fは，それぞれ異なった境界条件・初期条件で行った数値実験について，平衡状態に至るまでの流速の変化を平面上にプロットし，アニメーションにしたものである．

初期値としてABの近傍の点で表される状態を与えると，それぞれAB2上の点で表される定常状態になり（図7，，），BCとBC2の近傍の点で表される初期状態を与えるとBC上の点で定常状態になる（図7，，）．

図 7. ２本並列モデルの定常解と数値実験結果のアニメーション

したがって，すなわち点Oで表される状態から平衡を保ちながら少しずつ流速を大きくすると流れの状態はO→A→Pn→Cn〜C→Dと変化し，逆に点Dの状態から平衡を保ちながら流速を小さくすると，D→B〜Bn→Pn→A→Oと変化することがわかる．ここで→は平衡状態，〜は非平衡状態を経ることを表し，B1とB2をまとめてBn，C1とC2をまとめてCn，P1とP2をまとめてPnと記した．の範囲では，の状態からを大きくしていったのか，の状態からを小さくしていったのかということによってどの状態をとるかが決定する履歴現象が見られる．