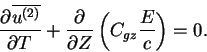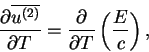|
ここでは Whitham (1974) に従って,
地形性β効果の係数 η が場所 z の関数である場合の
ロスビー波の性質について議論する.
回転円筒モデル中のロスビー波を表す式は,
浮力項と粘性項を無視した渦度方程式である.
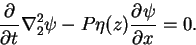 |
(D.1) |
この方程式の解を次のような波型の解として
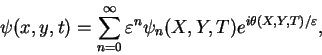
|
(D.2) |
を考える. ただし ε は微小なパラメターであり,
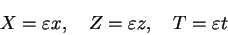
|
(D.3) |
はゆっくりとした変化を表す座標である.
地形性β効果を表す項 η はゆっくりと変化するものとする.
すなわち η=η(Z) である.
上記の波型の解の表現は実際にはその実数部のみ意味があることを
2 次の量を計算する際に気をつけなければならない.
(D.2)を(D.1) に代入して ε の次数で整理する.
O(ε0) から局所分散関係が求められる.
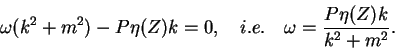
| (D.4) |
ただしω, k, m は局所的振動数および波数であり
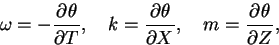
| (D.5) |
で定義される.
この定義から振動数および波数の保存則が導かれる.
分散関係を ω=Ω(k,m,Z) と書くと,
となる. ただし
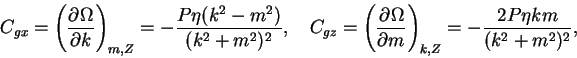
|
(D.9) |
は局所的な群速度である.
振動数と x 方向の波数は群速度とともに動く系でみて保存するが
z 方向の波数 m は保存しないことに注意されたい.
O(ε1) から振幅の式が得られる.
| | |
![$\displaystyle [\omega(k^2 + m^2) -P\eta(Z)k]\psi_1
-(k^2+m^2)\DP{\psi_0}{T} + [2k\omega-\eta(Z)]\DP{\psi_0}{X}
+ 2m\omega\DP{\psi_0}{Z}$](amp11.gif)
|
|
| | |
![$\displaystyle + \left[-\DP{}{T}(k^2+m^2)
+ \omega\DP{k}{X} + \omega\DP{m}{Z} \right]\psi_0 =0.$](amp12.gif)
|
(D.10) |
ψ1 の項は分散関係より消える.
残りの項の係数を振動数と波数の関係を用いて変形していくと
![$\displaystyle -\DP{}{T}[(k^2+m^2)\vert\psi_0\vert^2]
+ \DP{}{X}[(2k\omega-\eta(Z))\vert\psi_0\vert^2]
+ \DP{}{Z}(2\omega m\vert\psi_0\vert^2) =0.$](amp2.gif)
| | |
(D.11) |
ここで 1 波長平均した運動エネルギー
E=(k2+m2)|ψ0|2/4
を導入し, 群速度を用いて書き直すと
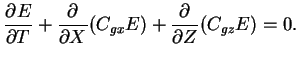
| | |
(D.12) |
となる. すなわち E は保存する.
このような振幅に関する保存則を導くには
実は変分法を用いる方が簡単で見通しが良い(Whitham, 1974).
その導出からこの E は本来波の作用と呼ぶべき量であることがわかる.
波が Z 方向に定常に伝播している状態では
CgzE が一定でなければならないので
ψ0〜1/√m(z) の程度に振幅が変化することがわかる.
しかしながら
「ロスビー波による解釈(2)-- 粘性の効果」
でのロスビー波の伝播距離を調べるときには,
たいして変化がないのでこのような効果を考えていない.
振動数, 波数の保存則と運動エネルギーの保存の式を組み合わせると
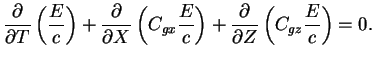
| | |
(D.13) |
となる. ここで c=ω/k は
x 方向の位相速度である.
E/c も波ともに群速度で運ばれていくことがわかる.
E/c は実はロスビー波に伴う振幅に関して
2 次のオーダーの運動量である.
そのためにもともとの運動方程式の x 成分
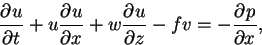
|
(D.14) |
を変形してみる.
ここで u, w はそれぞれ速度の x,z 成分である.
u を波の部分 u' とそれに伴う振幅の 2 次の速度
u(2) の和として表す.
u=u'+u(2) を代入し,
波が x 方向に単色であるとして
x 方向に平均をとると
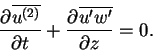
|
(D.15) |
なる式が得られる. ここで
![\begin{displaymath}
\overline{u'w'}
= -\overline{Re\left[\DP{\psi}{z}\right]\...
...right]}
= -\frac{km\vert\psi_0\vert^2}{2}
= C_{gz}\frac{E}{c}
\end{displaymath}](upwpbar.gif)
| (D.16) |
であるから,
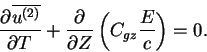
|
(D.17) |
さらに x 方向に平均した E/c の保存則を用いると
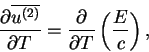
|
(D.18) |
したがってロスビー波に伴う 2 次の平均流,
すなわち運動量が E/c であることがわかる.
この場合ロスビー波の位相速度は常に正なので,
ロスビー波に伴う運動量は正である.
|
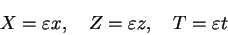
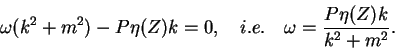
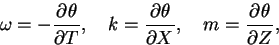
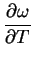
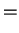
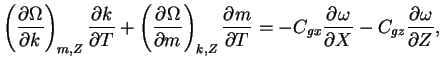
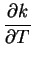
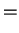
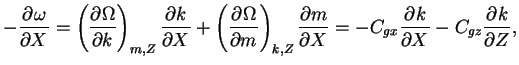
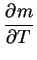
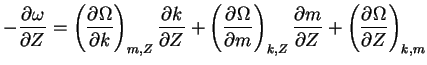
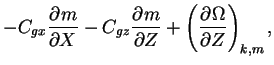
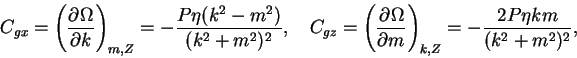
![$\displaystyle [\omega(k^2 + m^2) -P\eta(Z)k]\psi_1
-(k^2+m^2)\DP{\psi_0}{T} + [2k\omega-\eta(Z)]\DP{\psi_0}{X}
+ 2m\omega\DP{\psi_0}{Z}$](amp11.gif)
![$\displaystyle + \left[-\DP{}{T}(k^2+m^2)
+ \omega\DP{k}{X} + \omega\DP{m}{Z} \right]\psi_0 =0.$](amp12.gif)
![$\displaystyle -\DP{}{T}[(k^2+m^2)\vert\psi_0\vert^2]
+ \DP{}{X}[(2k\omega-\eta(Z))\vert\psi_0\vert^2]
+ \DP{}{Z}(2\omega m\vert\psi_0\vert^2) =0.$](amp2.gif)
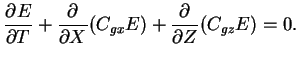
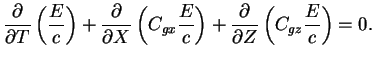
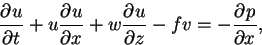
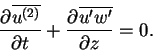
![\begin{displaymath}
\overline{u'w'}
= -\overline{Re\left[\DP{\psi}{z}\right]\...
...right]}
= -\frac{km\vert\psi_0\vert^2}{2}
= C_{gz}\frac{E}{c}
\end{displaymath}](upwpbar.gif)