Ue (θ) =境界層外縁における局所流速のコード方向成分（2
Q∞
cosΛ ×sinθ）
Ve (θ) =
境界層外縁における局所流速のスパン方向成分=
V∞
Qe (cc) =境界層外縁における局所流速
（[Ue2+ Ve2]
1/2）
δ (θ) = 境界層の特性厚さ （[νmD /2/(dUe
/dθ)] 1/2, δ(θ=0)= [νD /4Q∞cosΛ]
1/2
）
RQ (Q∞
)= 一様流レイノルズ数（ Q∞ L/
ν）
R (Q∞
,θ)=局所レイノルズ数（
Qeδ/ν
= Q∞ δ[1+ cos2Λ(4sin2θ-1)]
1/2
/ν）
R0(Q∞
,θ)=付着線レイノルズ数=スパン方向レイノルズ数（V∞δ/ν
= Ve δ/ν）
R1(Q∞
,θ)=コード方向レイノルズ数（Ueδ/ν）
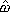 = 無次元角周波数（2πf
L/(Q∞ ×RQ1/2
)）
ξ(θ)=付着線からの外部流線の角度（R1/R0）
X =コード方向の無次元長（θD /2）
Y = スパン方向の無次元長（2y/πD）
Z =無次元高さ（z/δ）
<q > (θ,Y ,Z ,t,f ) =アンサンブル平均をとった速度変動
（ A(θ,Z ,Y ,f )sin(2πf t +φ(θ,Y ,Z ,f
)
）
A(θ,Y ,Z ,f )=速度変動の振幅
Amax(θ, f
)=速度変動の最大振幅
φ (θ, Y ,Z ,f
) =スピーカ入力信号を基準とする位相
A1(Y )，
A２(Y
)
=Mode1およびMode2の振幅分布（
a i2cos2(biY
-Y
i)；i=1,2
）
φ1 (Y ) ，φ２(Y
)
=Mode1およびMode2の位相分布
A*(Y )=合成された振幅分布
φ*(Y )=合成された位相分布
λ=撹乱の波長
Ψ=θ軸からの撹乱の伝播方向
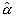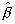 =コード方向の波数（2πLcosΨ/λ/RQ1/2）
 =スパン方向の波数（2πLsinΨ/λ/RQ1/2）
N =べき級数展開の打ち切り項数
|
