| 付録B.撹乱伝播に関する理論による予測 |
後退円柱の付着線近傍境界層に対する安定計算および発達する不安定撹乱の性質に関する理論的な予測を以下にまとめる.詳細については文献を参照されたい.
後退円柱上の三次元境界層において変曲点型の横流れ(C-F)不安定が支配的となることは古くからよく知られている11).近年,流れの非平行性を考慮に入れた安定性方程式を解くことにより新たな不安定モードの増幅が予測された.この新しい不安定は,壁面に平行な平面内の流線の曲率に起因する遠心力型不安定で,流線曲率(S-C)不安定と呼ばれている2-5) .
付着線近傍の流れの安定性は,2種類の方法で求められている.1つはOrr-Sommerfeld方程式に壁面曲率と外部流線の曲率および非平行性を付け加えたモデル方程式の固有値問題として扱う方法である2-5).臨界レイノルズ数が付着線から離れるに従って大きく減少したのち増加に転じる傾向を持つことはこの方法で近似的に予測された(図1a).もう一方は後退Hiemenz流れに対して厳密に導かれる偏微分線形撹乱方程式の級数解を求める方法である9) .この方法で得られる解は,付着線からの距離の逆数で展開されているために,付着線のごく近傍では発散してしまう(図15).従って,現状では付着線近傍境界層に対する臨界レイノルズ数の下流方向変化(臨界曲線)を正確に予測できているとは言えない.
増幅する撹乱の性質は複素特性曲線法に基づく撹乱伝播理論で求められている.これまでの理解では三次元境界層における撹乱の伝播方向を唯一に定めることができなかったが,Itohの撹乱伝播理論2-5)では,解に物理的な実現条件を課す方法で,撹乱の伝播方向が一意的に決定され,結果的に撹乱の発達を精度良く記述できるようになった.
この理論によると, 後退円柱上の境界層では,周波数,が正の値をもつC-Fモードは外部流線の外向きに伝播し,負の周波数を持つS-Cモードは,波数ベクトルと逆向き(外部流線の内向き)に伝播する(図16).符号を無視すれば増幅する周波数帯域は重複するが,最大増幅する周波数はC-F不安定の方が2倍ほど高い.また絶対値が同じ周波数の撹乱であれば,スパン方向の波数はC-Fモードの方がS-Cモードよりも倍以上大きい.2種類の不安定性で傾向が大きく異なるもう一つの特性として境界層方向の位相分布が挙げられる.図17に示す通り,振幅分布は両者が非常に近い分布を取るのに対し,位相分布の特性は大きく異なる.C-Fモードは壁面近くにおいて位相が境界層外縁より150°程度も進んでいる.すなわち位相遅れ(図17中:phase)が小さい.一方S-Cモードの位相分布は反対の勾配を持ち外縁と壁面近傍の差も60°程度と小さい.上記した2つの相違点は後退角やレイノルズ数には依存しないことがわかっている2-5).
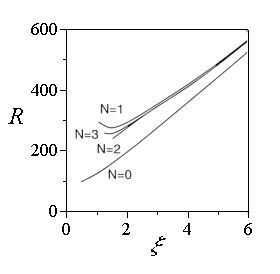
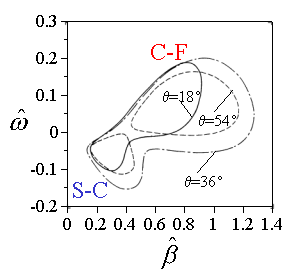
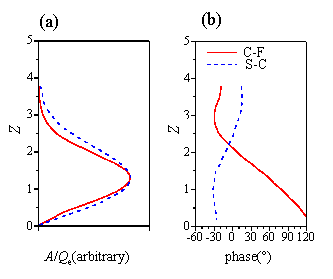
図17 境界層方向の振幅と位相分布( Λ=50゜, RQ= 0.5×106 ,θ=54゜,C-F:
=0.09;Y=0.21,S-C:
=-0.03;Y=0.18)4).