5.3 流体の鉛直方向の運動を仮定する

図12 時刻t₁に上昇を始めた流体が,
時刻tにリングに到達する.

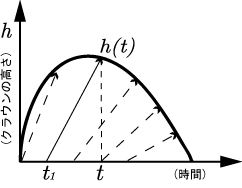
前節では，時刻tに付け根から上端まで，壁の中を（5）式で表される速度を保ったまま，等速的に上昇するとした． ここでさらに次の仮定をする．

上昇した流体は，壁を等速的に上昇し，やがてクラウンの上端に達する．上端に達した流体は，そのまま上端に溜まり， リングを形成すると仮定する．時刻t₁ に上昇を始めた流体が， 時刻 t に高さ h(t) に達するとする．（概念図を図12に示す．）上昇速度は（5）式で表わされると仮定しているので，t₁に関して次式が成り立つ．

（6）

壁を上昇する流体には，クラウンによって押し退けられた流体層と，流体層に衝突した液滴の２つが考えられる．衝突した液滴のうち，上端に達した体積をVとすると，リングの半径r_crに関して，次の関係が成り立つ．

（7）

と表せる．ここでは液滴のうち，水面下に沈んだ部分と同じ体積が，押し退けられた流体と同じ速度で上昇すると考えることにより，Ｖ　を求めることにする．

（2）〜（7）式を組み合わせれば，ある初期値に対して，クラウンの高さを計算する事ができる．