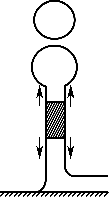5.2 上昇速度を仮定する

図11 壁では表面張力の鉛直成分が釣り合う

図10のモデルからクラウンの高さを計算するには，クラウンの上端にある流体の半径ｒを求めることが必要である．

 図11に，クラウンの鉛直断面の概念図を示す．（図10では考えなかった，クラウンの壁の厚みに注目する．）壁の鉛直断面の厚さが，高さによらず一定であると仮定する． このとき，壁内の流体には，表面張力と重力のみが働いている．表面張力は上下で釣り合うから，壁内の流体にかかる力は，重力だけであると考えてよい． 

実験で得られた画像では，クラウンの内側で，ガラス面が見えているものがあることから考えると，クラウンの内側にあった流体は，クラウンによって完全に押し退けられていると考えられる．押し退けられた流体は，落下した液滴とともにクラウンの壁及びリングを形成していると考えられる． このとき，クラウンの付け根での流体の収支は，

（3）

と表される．但しdは流体の深さ，δは壁の厚さ，r_crはクラウンの半径，ｖは付け根から流体が上昇する速度である． の値は，1m/sのオーダーである．流体の深さに比べ，壁の厚さは小さいと考えられるから，vのオーダーは，1m/s以上である．

これに対し，考えている現象の時間スケールは1ms程度であり，この時間で重力による加（減）速は，0.01m/s程度であり，2桁以上小さい．従って，壁の中の流体は，等速運動をすると考えて良い．

4.3節で示したように，クラウンの直径は，時間の1/4乗に比例し，Crを比例定数として，

（4）

と表せる．t=0を，衝突した液滴の半分が沈んだ瞬間と定義すると，この瞬間のクラウンの半径は，液滴の半径に等しく2mmであると考えられる．このときt₀は，t=0でr_cr=2mmにするための，時間の原点のずれを表す定数である．

（4）式に従えば，付け根に流入する流体の速度は（t-t₀）の-3/4乗に比例する．（3）式で，壁の厚さδが時間によらず一定であるとすれば，付け根から上昇する流体の速度も-3/4乗に比例して，

（5）

と表せる．ここで，C₁= Cr　d / 4　δ である．