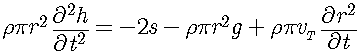5.1 鉛直方向の運動方程式

図10 考えたモデルの断面図

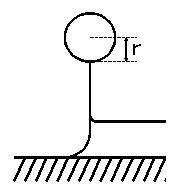
解析では，クラウンの高さの変化から見積もられる鉛直方向の加速度は，上昇時と下降時で大きく異なっていることがわかった．このことを簡略化したモデルを用いて検証する．

図10のように，クラウンの上端が，半径ｒの円柱が環状に曲がったような構造（この部分を，以降リングと呼ぶ ）をしているとし，流体にかかる力は重力と表面張力だけであるとする．

表面張力をs，重力加速度をg，流体の密度をρ，壁の上端（リングの下端）での流速をv_T，リングの（中心の）高さをhとする．表面張力は，クラウンの内・外側の2面でかかるので，運動方程式は 次のように表すことができる．

（2）

右辺の3項目は，壁から流入する運動量をあらわす．

この式の妥当性を，画像解析による値で簡単に検証してみる．
標準実験ではd²h/dt²の値は，クラウンの高さが最大になる時でおよそ -100 m/s²である．そこで，クラウンの高さが最大となる時の加速度を -100 m/s² と仮定し，牛乳の表面張力を 50 dyn/cm ，密度を 1g/cm³ とすれば，(2)式から求められるリングの半径は，ｒ = 0.6 mm となる．

画像からリングの半径を見積もることにする．画像からは断面を見る事はできないが，画像に写ったクラウンの左右の端にある突起の付け根の太さは，リングの直径にほぼ等しいと考えられる．標準実験で高さが最大となったD01C00でこの部分の大きさを測ると，およそ 0.8mm であり，上の見積もりとほぼ一致した．

そこで，クラウン上端の流体に対して（2)式が成り立つとして，以下の議論を進めることにする．