4.3　表面張力波解

これまでは，ミルククラウンのような現象は，これまでは主として表面張力波として考えられてきた．Yalin and Weiss (1995) の様に，ミルククラウンの様な軸対称の構造を仮定し，浅水系で支配方程式を解けば，クラウンの半径ｒ_crは，αを定数として，

（1）

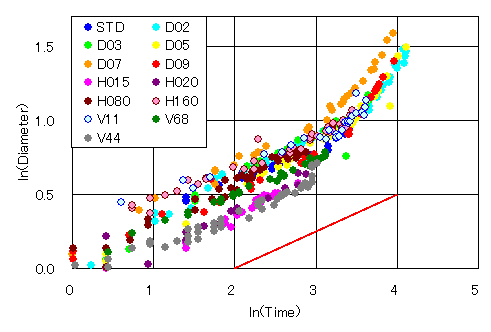
の形で表され，時間の1/2乗に比例することが知られている．t₀は，時間の原点のずれを表す定数である． この関係は，擾乱が鉛直方向に一定の速度で引き戻されると仮定すれば，質量保存の関係から求めることもできる（ Fulana and Zaleski (1998) ）．

本実験の時間および直径の対数を取ったグラフを図7に示す． この図を見ると，クラウン崩壊前のｔ < 30ms の領域では，どの条件でもグラフの傾きはおよそ1/4 であることがわかる．この傾きは，t₀を-5ms<t₀<5msで変化させてもほとんど変化しない．

また，クラウン崩壊後の傾きは，崩壊前と明らかに異なっていることがわかる．これについては，次ページで別途解析する．

図7 クラウンの直径の時間変化(両対数グラフ) 赤実線は，傾きが1/4の直線を示す．