E 順圧不安定
基本流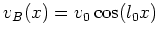 が、
が、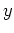 方向の波数
方向の波数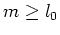 の擾乱に対して安定であることを証明する。なお、この章では証明を見易くするため、波数を
の擾乱に対して安定であることを証明する。なお、この章では証明を見易くするため、波数を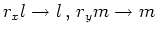 と置き換えている。また、粘性の影響を明確にするため、動粘性係数
と置き換えている。また、粘性の影響を明確にするため、動粘性係数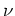 (本研究では1)を表示している。
(本研究では1)を表示している。
順圧成分について考えるので、基礎方程式の(1),(2),(5)において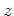 微分を0とすると
微分を0とすると
ただし、
ここで、流線関数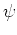 を次のように定義する。
を次のように定義する。
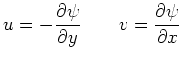 |
(60) |
また、渦度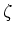 を次で定義する。
を次で定義する。
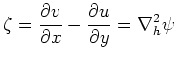 |
(61) |
式(57),(58)より、渦度方程式は
式(59),(61)を用いて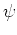 のみで表すと次のようになる。
のみで表すと次のようになる。
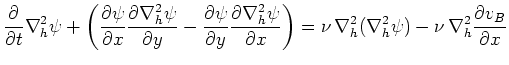 |
(62) |
渦度方程式(62)は次の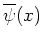 を定常解として持つ。
を定常解として持つ。
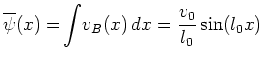 |
(63) |
この基本流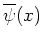 に摂動
に摂動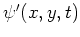 を与えた場合、摂動方程式は線形化して次のようになる。
を与えた場合、摂動方程式は線形化して次のようになる。
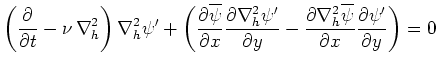 |
(64) |
ここで、領域積分の記号を次で定める。
式(64)の両辺に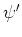 を掛けて領域積分し、部分積分を行うと擾乱のエネルギー
を掛けて領域積分し、部分積分を行うと擾乱のエネルギー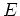 に関する次式を得る。
に関する次式を得る。
また、式(64)の両辺に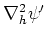 を掛けて同様の操作を行うと擾乱のエンストロフィー
を掛けて同様の操作を行うと擾乱のエンストロフィー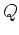 に関する次式を得る。
に関する次式を得る。
ここで(63)より
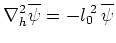 |
(67) |
よって、次の関係が得られる。
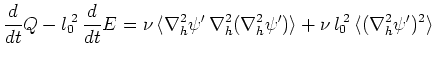 |
(68) |
ここで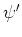 を
を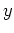 方向の波数
方向の波数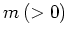 の摂動としてスペクトル展開する。
の摂動としてスペクトル展開する。
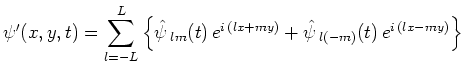 |
(69) |
すると、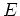 は次のように書ける。
は次のように書ける。
同様にして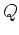 や(68)の右辺第1項は次のようになる。
や(68)の右辺第1項は次のようになる。
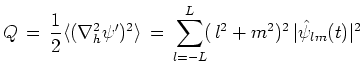 |
(71) |
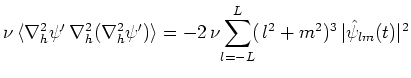 |
(72) |
(70),(71),(72)を(68)に代入し、さらに
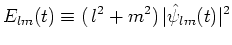 |
(73) |
を導入すると、次の式が得られる。
![$\displaystyle \sum_{l=-L}^{L}[\,(\,l^2+m^2)\,-l_0\,\!\!^2\,]\frac{d}{dt}E_{lm}(...
...2\,\nu \!\!\sum_{l=-L}^{L}[\,(\,l^2+m^2)^2-l_0\,\!\!^2(\,l^2+m^2)\,\,]E_{lm}(t)$](img382.png) |
(74) |
さて、基本流が線形不安定であるとき、(64)は発達する固有モードを持つ。その発達率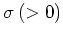 を用いて、
を用いて、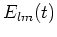 の時間変化は
の時間変化は
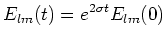 |
(75) |
と表せる。(75)を(74)に代入すれば、
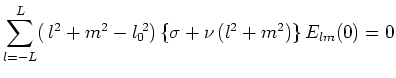 |
(76) |
を得る。したがって、擾乱が発達するための必要条件は、「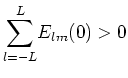 かつ
かつ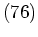 が成立」となる。
が成立」となる。
- i)
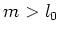 の擾乱
の擾乱
-
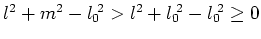 より、(76)の
より、(76)の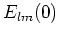 の係数は全ての
の係数は全ての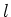 について正である。したがって、
について正である。したがって、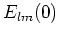 は全て0になり、擾乱は発達しない。
は全て0になり、擾乱は発達しない。
- ii)
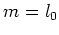 の擾乱
の擾乱
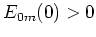 ,
,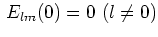 の場合にのみ必要条件が満たされる。これは初期擾乱が
の場合にのみ必要条件が満たされる。これは初期擾乱が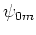 モード単独であることを意味しているが、このとき(64)は左辺第2項の括弧内が0となり、
モード単独であることを意味しているが、このとき(64)は左辺第2項の括弧内が0となり、
のように拡散方程式の形になるため、擾乱は発達しない。
i),ii)より、基本流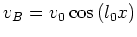 は
は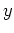 方向の波数
方向の波数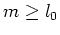 の擾乱に対して安定である。
の擾乱に対して安定である。
この結果より、基本流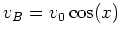 は
は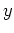 方向の波数
方向の波数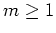 の擾乱に対して安定である。波数の表記を元に戻すと、基本流
の擾乱に対して安定である。波数の表記を元に戻すと、基本流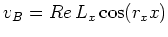 は
は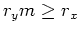 の擾乱に対して安定である。本研究では
の擾乱に対して安定である。本研究では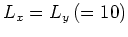 なので
なので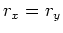 より、
より、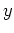 方向の波数
方向の波数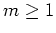 の擾乱に対して安定となる。
の擾乱に対して安定となる。
SAITO Naoaki
2008-03-07
![]() 微分を0とすると
微分を0とすると
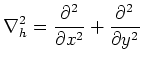
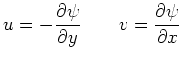
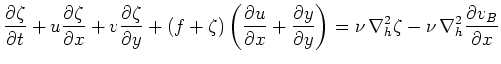
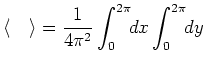
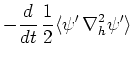
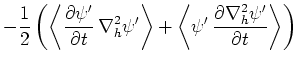
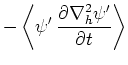
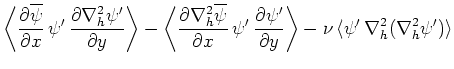
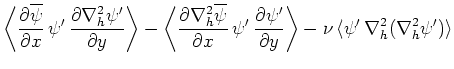
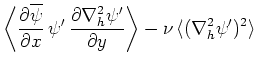
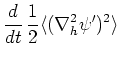
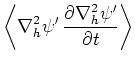
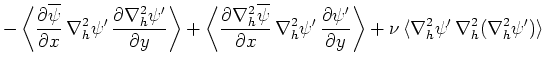
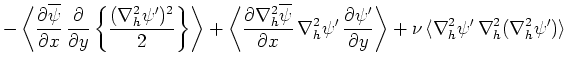
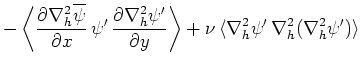
![]() を
を![]() 方向の波数
方向の波数![]() の摂動としてスペクトル展開する。
の摂動としてスペクトル展開する。
![]() を用いて、
を用いて、![]() の時間変化は
の時間変化は
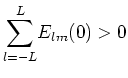 かつ
かつ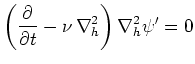
![]() は
は![]() 方向の波数
方向の波数![]() の擾乱に対して安定である。波数の表記を元に戻すと、基本流
の擾乱に対して安定である。波数の表記を元に戻すと、基本流![]() は
は![]() の擾乱に対して安定である。本研究では
の擾乱に対して安定である。本研究では![]() なので
なので![]() より、
より、![]() 方向の波数
方向の波数![]() の擾乱に対して安定となる。
の擾乱に対して安定となる。