付録 D. 交差モードの水平構造

本文 5.3 節では, 慣性不安定領域の北側に計算領域が存在する場合の東進交差モードの構造が議 論された. そこでは, 交差モードは北側境界付近で大きな振幅をもつことが 示された. その他の場合でも, 交差モードは同様な構造を持つ. すなわち, 慣性不安定領域の北側(南側)に計算領域が存在する場合は 交差モードは北側(南側)境界付近で大きな振幅をもつ. この性質は E の値によらない. E の値が小さく交差モードが他の重力波の分散曲線と 交差を起こしていない場合でも, 上記の性質は変わらない.

以下では様々な場合について交差モードの構造を示し 上記のことを示す.

E が大きく, 慣性不安定領域の北側に計算領域が存在する場合

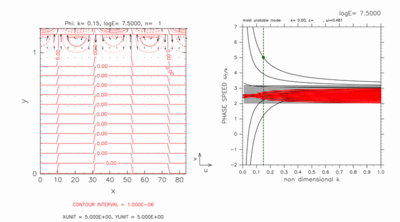
図 D-1, D-2 に, log E=7.50 に対して, 計算領域として 0.0 < y < 1.2 を取った場合の結果を示す. これは, 慣性不安定領域の北側に格子点が 2 つ存在する場合である. この E の値では通常の中立モードは全て c=2.5 (力学的赤道における基本場の流速値)に漸近してしまい (cf. Clark and Haynes, 1996) 連続モードの分差曲線の束の外には交差モードの分散曲線のみが残っている.

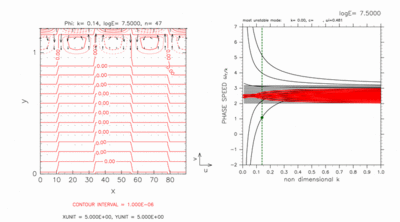
図 D-1 は 5.3 節で示した東進交差 モードである. 西進交差モード(図D-2)も北側境界付近で大きな振幅を持つ.

[動画] [動画]

図D-1: 図8と同様の, 東進交差モードの分散曲線(右図)と水平構造(左図)の図. log E=7.50, k=0.15 の場合. 水平構造の図の等値線間隔は, 1.0 × 10-6 である. [動画]をクリックすると, c=5.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の右図の分散曲線では, 交差モードは緑●印で表している. アニメーション図の左図の等値線間隔は, 1.0 × 10-6 (k=0.15 の場合), 5.0 × 10-6 (k=0.07 の場合) である.

図D-2: 図D-1と同様の図. ただし, k=0.14 の場合の西進交差モードの図. 水平構造の図の等値線間隔は, 1.0 × 10-6 である. [動画]をクリックすると, c=1.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の左図の等値線間隔は, 3.0 × 10-6 (k=0.06 の場合), 1.0 × 10-6 (k=0.14 の場合) である.

E が大きく, 慣性不安定領域の南側に計算領域が存在する場合

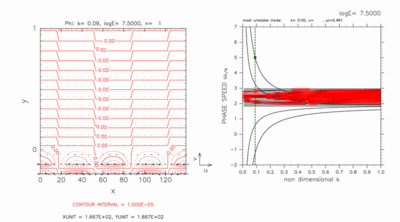
図 D-3, D-4 に, log E=7.50 に対して, 計算領域として -0.2 < y < 1.0 を取った場合の結果を示す. これは, 慣性不安定領域の南側に格子点が 2 つ存在する場合である. この E の値では通常の中立モードは全て c=2.5 (力学的赤道における基本場の流速値)に漸近してしまい (cf. Clark and Haynes, 1996) 連続モードの分差曲線の束の外には交差モードの分散曲線のみが残っている.

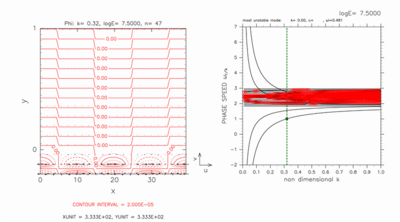
東進交差モード(図 D-3)も西進交差モード(図 D-4)も 南側境界付近で大きな振幅を持つ.

[動画] [動画]

図D-3: 図D-1と同様の図. ただし, 計算領域 -0.2 < y < 1.0, k=0.09 の場合の東進交差モードの図. 水平構造の図の等値線間隔は, 1.0 × 10-5 である. [動画]をクリックすると, c=5.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の左図の等値線間隔は, 1.0 × 10-5 (k=0.09 の場合), 4.0 × 10-7 (k=0.04 の場合) である.

図D-4: 図D-3と同様の図. ただし, k=0.32 の場合の西進交差モードの図. 水平構造の図の等値線間隔は, 2.0 × 10-5 である. [動画]をクリックすると, c=1.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の左図の等値線間隔は, 4.0 × 10-7 (k=0.13 の場合), 2.0 × 10-5 (k=0.32 の場合) である.

E が小さく, 慣性不安定領域の北側に計算領域が存在する場合

図 D-5, D-6 に, log E=3.50 に対して, 計算領域として 0.0 < y < 1.2 を取った場合の結果を示す. この場合では, 慣性不安定領域の北側に格子点が 2 つ存在している. この E の値では交差モードの分散曲線は隣接する他の重力波の分散 曲線との交差を起こしていない. 連続モードの分差曲線の束の外には, 通常の中立モードと交差モードの分散曲線が ともに存在している.

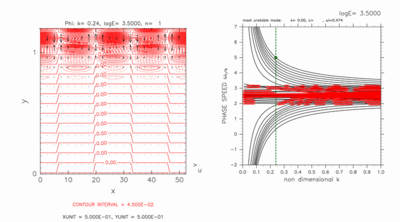
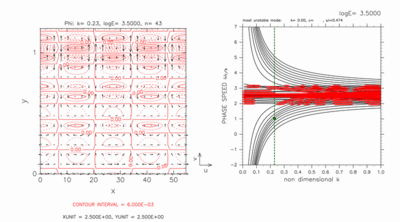
図 D-5, D-6 の分散曲線のみではどれが交差モードの分散曲線か判別できないが, E の値を少しずつ増加させて 交差モードの分散曲線だけが残った状態まで分散曲線図を追跡することにより, 交差モードの分散曲線を同定することが出来る. この場合, 東進交差モードの分散曲線(図D-5)は中立モードの分散曲線の外側に2つ存在し, 西進交差モードの分散曲線(図D-6)は中立モードの分散曲線の束の中に2つ存在する.

分散曲線が交差を起こしていなくても 東進交差モード(図D-5)も西進交差モード(図D-6)も 北側境界付近で大きな振幅を持つ.

[動画] [動画]

図D-5: 図D-1と同様の, log E=3.50, k=0.24 の場合の 東進交差モードの図. 水平構造の図の等値線間隔は, 4.5 × 10-2 である. [動画]をクリックすると, c=5.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の右図の分散曲線では, 交差モード以外のモードは青●印, 交差モードは緑●印で表している. アニメーション図の左図の等値線間隔は, 全て 4.5 × 10-2 である.

図D-6: 図D-5と同様の, k=0.23 の場合の西進交差モードの図. 水平構造の図の等値線間隔は, 6.0 × 10-3 である. [動画]をクリックすると, c=1.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の左図の等値線間隔は, 全て 6.0 × 10-3 である.

E が小さく, 慣性不安定領域の南側に計算領域が存在する場合

図 D-7, D-8 に, log E=2.30 に対して, 計算領域として -0.2 < y < 1.0 を取った場合の結果を示す. この場合では, 慣性不安定領域の南側に格子点が 2 つ存在している. この E の値では交差モードの分散曲線は他の曲線との 交差を起こしていない. 連続モードの分差曲線の束の外には, 通常の中立モードと交差モードの分散曲線が ともに存在している.

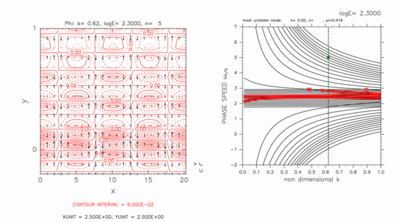
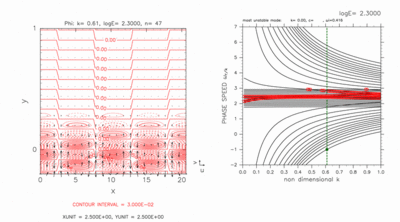
図 D-7, D-8 の分散曲線のみでは交差モードを判別することができないが, 図 D-5, D-6 の場合と同様に, E を少しずつ増加させて 交差モードの分散曲線だけが残った状態まで追跡することにより, 交差モードの分散曲線を同定することができる. この場合, 東進交差モードの分散曲線(図D-7)は中立モードの分散曲線の束の中に2つ存在し, 西進交差モードの分散曲線(図D-8)は中立モードの分散曲線の外側に2つ存在する.

分散曲線が交差を起こしていなくても 東進交差モード(図D-7)も西進交差モード(図D-8)も 南側境界付近で大きな振幅を持つ.

[動画] [動画]

図D-7: 図D-3と同様の図. ただし log E=2.30, k=0.62 の場合の東進交差モードの図. 水平構造の図の等値線間隔は, 9.0 × 10-2 である. [動画]をクリックすると, c=5.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の右図の分散曲線では, 交差モード以外のモードは青●印, 交差モードは緑●印で表している. アニメーション図の左図の等値線間隔は, 全て 9.0 × 10-2 である.

図D-8: 図D-7と同様の, k=0.61 の場合の西進交差モードの図. 水平構造の図の等値線間隔は, 3.0 × 10-2 である. [動画]をクリックすると, c=-1.00 付近のモードの構造を走査したアニ メーション図を見ることが出来る. アニメーション図の左図の等値線間隔は, 全て 3.0 × 10-2 である.

付録 D. 交差モードの水平構造