5. 分散曲線が交差を起こす中立モードの性質

5.1 目的

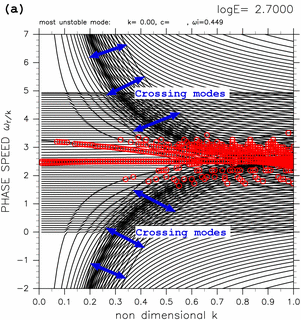
TI2006 が示した E の値が大きい場合の分散曲線図においては, 隣り合う分散曲線が交差を起こす中立モードが存在していた. 分散曲線が交差を起こしている例を図6 に示す. 東進・西進慣性重力波モードの分散曲線に重なって存在する 図中の青矢印で示された分散曲線が 隣接する分散曲線と交差を起こしている. 以下では, 隣接する分散曲線の交差を引き起こす中立モードを 「交差モード」と呼ぶことにする. 交差モードは以下の性質を持っている.

• 符号が異なる擬運動量を持つモードの分散曲線と交差を起こしても, 不安定にならない. 連続モードは負の擬運動量を持ち (Iga, 1999a), 図6(a), (b) の青矢印で示された東進する交差モードは正の擬運動量を持つ (Iga, 1999b). これらの分散曲線の交差により共鳴が起こっても良いはずであるが, 両者の共鳴による不安定は発生していない (解像度を 10 倍にした計算でも結果は変わらない. 図は示さない).
• E が増加した場合でも位相速度の値が c=2.5 に漸近しない. シアー流中の赤道波の位相速度は, E が大きくなるにつれて力学的赤道における基本場の流速値に漸近する (Clark and Haynes, 1996). しかし, 交差モードはこの漸近値を飛び越えた位相速度を持つ. 図6 の青矢印で示された東進する交差モードの位相速度は, 東西波数が大きい時に 2.5 以下になっている. また, 西進する交差モードの位相速度は東西波数が大きい時に 2.5 以上になっている.

TI2006 では, 交差モードに関して何も言及されていなかった. 以下では, 交差モードの発生条件および水平構造に関して調査を行った結果を示す.

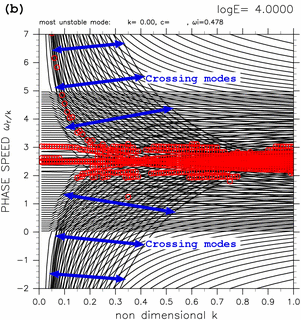図6: (a) log E=+2.70 の場合, (b) log E=+4.00 の場合の分散曲線. 青矢印は交差モードの分散曲線が存在する範囲を示す. その他の図中の記号の意味は表1と同じ. 図をクリックすると拡大図を見ることができる.

5.2 交差モードの分散曲線が発生する条件

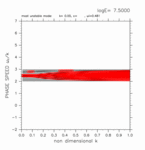
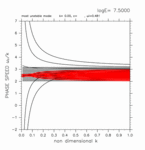
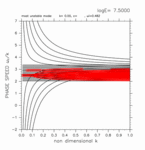
計算領域の幅を様々に変える計算を行ったところ, 慣性不安定領域の外側の領域の存在が交差モードをもたらす ことがわかった. 図7 に, 計算領域として慣性不安定領域のみを考えた場合から 計算領域の幅を広くしていった場合の結果を示す. 図7 には, 交差モードの分散曲線を良く観察することのできる E が大きい場合の結果を示している. 図7(左) は計算領域が慣性不安定領域のみを含む場合 の結果であり, ここでは交差モードは出現していない. 図7(中) は, 慣性不安定領域の北外側に 2 つ の格子点が存在する場合の分散曲線である. この場合, 東進の交差モード, 西進の交差モードの数はそれぞれ 2 つになっている. 図7(右) の場合では, 慣性不安定領域の外側に存在する 格子点は, 北側に 5 つあり, 東進・西進交差モードもそれぞれ 5 つ存在する. 図7 に示した場合以外にも順次計算領域の幅を増加させて いく計算(付録 B)もおこなったところ, 慣性不安定領域の外側の領域に格子点を 1 つ増やすと 東進の交差モード, 西進の交差モード, 連続モードの分散曲線が各々 1 つ増 えることがわかった. 逆に, 慣性不安定領域(0 ≤ y ≤ 1)だけを計算領域 とした場合には, 南北方向の格子点数に依らず交差モードは出現しないことも確認された (付録 C).

[動画]	[動画]	[動画]

図7: 計算領域を変えた場合の分散曲線図. (左) 計算領域が 0.0 < y < 1.0 の場合. (中) 計算領域が 0.0 < y < 1.2 の場合. (右) 計算領域が 0.0 < y < 1.4 の場合. 図で示してあるのは, log E=+7.50 の場合. 図をクリックすると拡大図を見ることができる. [動画]をクリックすると E を変化させた 分散曲線図のアニメーションを見ることができる. 記号の意味に関しては表1を参照されたい.

5.3 交差モードの水平構造

図8 に, 0.0 < y < 1.2 の計算領域において log E=7.50 を与えた場合の結果を示す. この場合には, 連続モードの分散曲線の束の外に 交差モードの分散曲線だけが残った状態になっている. 図8(左) に東進交差モードの水平構造を示す. 交差モードは, 慣性不安定領域の外側の領域 y > 1 において 大きな振幅を持つことが示されている. 同様に, 西進交差モードも y > 1 において大きな振幅を持つ ことも確認された (付録 D参照). E が小さい場合には, 交差モードの分散曲線は隣り合う分散曲線と交 差を起こしていないけれども, 慣性不安定領域の外側で交差モードの振幅が大きくなる ことが確認された(付録 D参照). このように, 慣性不安定領域の北側(南側)に計算領域が存在する場合には, 東 進, 西進であるかに依らず, 交差モードは慣性不安定領域の北側(南側)で大き な振幅を持つ. 以上より, 交差モードは慣性不安定領域の外側のチャネル領域に存在する 重力波的モードであろうと想像される. 赤道波というより中緯度β面の重力波的な 性質を持つモードなのであろう.

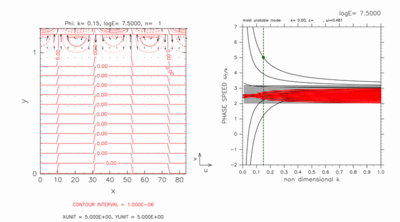
図8: log E=7.50, k=0.15 の交差モードの分散曲線(右図)と水平構造(左図). 計算領域を 0 < y < 1.2 した場合の結果. 右図の緑丸印のモードの水平構造を左図に示す. 左図のコンターはジオポテンシャル, ベクトルは速度場を表す. 水平構造の図の等値線間隔は, 1.0 × 10^-6 である. 右の分散曲線図の記号の意味に関しては表1を参照されたい. 図をクリックすると拡大図を見ることができる.

5. 分散曲線が交差を起こす中立モードの水平構造