TI2006 では 3 つの手法, (1) 赤道ケルビン波の近似分散関係式の導出, (2) 基本場の流速分布を部分的に変えることによる連続モードの分散曲線の除去 (Iga, 1999c の応用), (3) 一様Γ平面近似 (Boyd and Christdis, 1982) の適用による赤道波の近似分散関係式の導出, により, 共鳴を起こす赤道ケルビン波モードと混合ロスビー重力波モードの分 散曲線の同定を試みた. しかし, E が大きい場合には, これらのモードの分散曲線が 他の不安定モードの分散曲線と重なってしまうため その位置や振る舞いを分散曲線上でよく確認できない でいた.
5節で議論した 計算領域が 0 < y < 1 の場合では, 連続モードの位相速度の範囲は TI2006 よりも狭い. このため, 赤道ケルビン波モードと連続モードとの共鳴により発生する不 安定モードや混合ロスビー重力波モードの分散曲線が よく見えていた. ここでは, 計算領域を 0 < y < 1 とした場合において, 赤道ケルビン波モードと西進混合ロスビー重力波モード の分散曲線が接近した場合について, 分散曲線の振る舞いを詳細に観察した結果を示す. 計算領域を様々に変えた場合については 付録 B に示した.
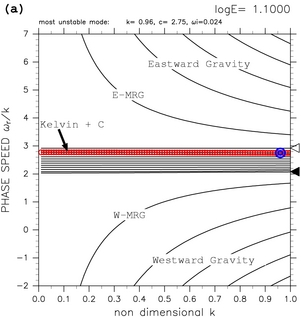
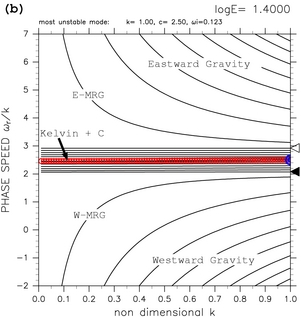
計算領域を 0 < y < 1, log E < 1.50 とした場合(図 9a, b) において, 赤道ケルビン波モードと連続モードとの共鳴によって発生した 不安定モードの位相速度は, E の増加に伴い c=2.5 (力学的赤道における基本場の流速値)に漸近していく. この結果は, 漸近展開により赤道域シアー流中のモードの分散曲線を 求めた Clark and Haynes (1996) の議論と調和的なものである. にもかかわらず, TI2006 が示した分散曲線図では 明瞭に確認することができなかったものである.
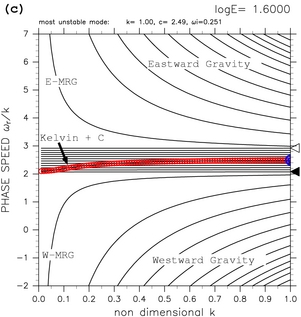
更に, E が大きくなると(図9c, 9d), 赤道ケルビン波モードと西進混合ロスビー重力波モードが共鳴を 起こす. TI2006 の結果 (彼らの figure 6f) では, この共鳴が起こる際に, 赤道ケルビン波モードと連続モードとの共鳴によって生じた不安定モードの 分散曲線が折れ曲がるように見えていた. TI2006 の分散曲線図では, 赤道ケルビン波モードと連続モードとの共鳴によって生じた不安定モードの 分散曲線が他のモードの分散曲線の中に完全に埋もれてしまっていたため, その変形具合をよく観察できないでいた. それに対して, 領域を 0 < y < 1 とした場合では, 赤道ケルビン波モードと連続モードの共鳴によって生じた不安定モードの 分散曲線が折れ曲がる様子を見ることができる(図 9c, 9d. log E=1.50 から log E=2.50 まで変化させた場合の分散曲線図の 動画 も参照されたい). 計算領域を 0 < y < 1 とした場合, 赤道ケルビン波モードと連続モードの共鳴によって生じた不安定モードの 分散曲線の変型が起こり始めるのは log E=1.60 である. この場合, k=0 の不安定モードが発生するのは log E=1.65 である. よって, TI2006 で予想されたように, 不安定モードの分散曲線の変形は, E が k=0 の不安定モードが 発生する値に近づくと起こり始めることが確認された.
k=0 の不安定モードが発生する時の E の値 が TI2006 と異なるのは, 計算領域が彼らのものと比べて狭いことが影響しているようである. 計算領域が -1 < y < 2 よりも広い場合には, log E=1.20 で k=0 の東西対称不安定モード(慣性不安定モード)が発生し, Stevens (1983) や TI2006 と同じ結果となる(図は示さない). しかし, 計算領域が -1 < y < 2 よりも狭い場合には 東西対称モードが発生する E の値は log E=1.20 からずれてし まう.
 |
 |
 |
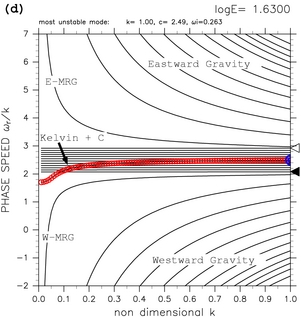 |
図9: 計算領域を 0.0 < y < 1.0 とした場合の分散曲線図. (a) log E=+1.10, (b) log E=+1.40, (c) log E=+1.60, (d) log E=+1.63 の場合を示す. 図中で "Kelvin + C" のラベルの付いた分散曲線は, 赤道ケルビン波モードと連 続モードの共鳴による不安定モードの分散曲線を示す. その他の記号については, 表1と同様である. log E=+1.50 から log E=+2.50 まで変化させた場合の分散曲線図の 動画 も参照されたい.