付録 B. 計算領域の南北幅を変えた場合の交差モードの数の変化

本文 5.2 節において, 慣性不安定領域の外側に計算領域を付与することにより 交差モードが発生することを議論した. 本節では, 計算領域が慣性不安定領域のみである場合から徐々に計算領域を 広げた結果を用いて, 計算領域の拡大により交差モードの数が順次増えて いくことを示す.

表B-1 は, 様々な計算領域を用いて得られた分散曲線図に応じて交差モード の数がどのように変化するかをまとめたものである. 各場合において示された画像は log E=7.50 を与えた場合の分散曲線図である. この E の値においては, 連続モードの分散曲線の束の外に 交差モードの分散曲線だけが残った状態になっている. 慣性不安定領域 0 ≤ y ≤ 1 の外に格子点を 1 つ増やすと, 東進の交差モード, 西進の交差モード, 連続モードの分散曲線が各々 1 つ増えて いくことがわかる.

計算領域・格子点数 ・分散曲線アニメーション図 交差モードの数 分散曲線(log E=7.50) +0.00 < y < +1.00 (grid 数 13) [動画] 東進: 0個 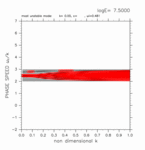西進: 0個 +0.00 < y < +1.20 (grid 数 16) [動画] 東進: 2個 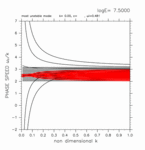西進: 2個 +0.00 < y < +1.40 (grid 数 19) [動画] 東進: 5個 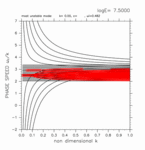西進: 5個 +0.00 < y < +1.60 (grid 数 22) [動画] 東進: 8個 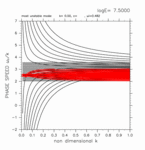西進: 8個 +0.00 < y < +1.80 (grid 数 25) [動画] 東進: 11個 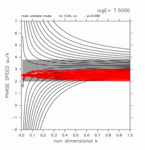西進: 11個 +0.00 < y < +2.00 (grid 数 28) [動画] 東進: 14個 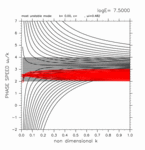西進: 14個 +0.00 < y < +2.20 (grid 数 31) [動画] 東進: 16個 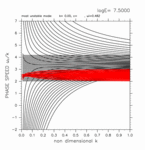西進: 16個 +0.00 < y < +2.40 (grid 数 34) [動画] 東進: 19個 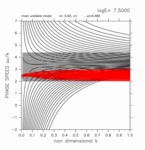西進: 19個 +0.00 < y < +2.60 (grid 数 37) [動画] 東進: 22個 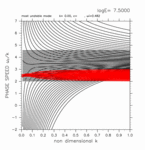西進: 22個 +0.00 < y < +2.80 (grid 数 40) [動画] 東進: 25個 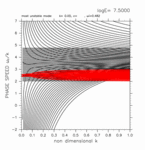西進: 25個 +0.00 < y < +3.00 (grid 数 43) [動画] 東進: 28個 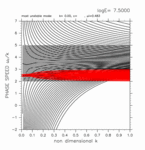西進: 28個

計算領域・格子点数 ・分散曲線アニメーション図 交差モードの数 分散曲線(log E=7.50) +0.00 < y < +1.00 (grid 数 13) [動画] 東進: 0個 西進: 0個 -0.20 < y < +1.00 (grid 数 16) [動画] 東進: 2個 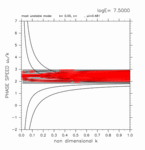西進: 2個 -0.40 < y < +1.00 (grid 数 19) [動画] 東進: 5個 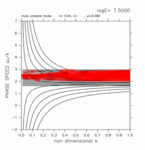西進: 5個 -0.60 < y < +1.00 (grid 数 22) [動画] 東進: 8個 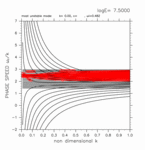西進: 8個 -0.80 < y < +1.00 (grid 数 25) [動画] 東進: 11個 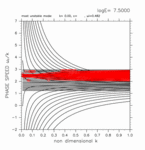西進: 11個 -1.00 < y < +1.00 (grid 数 28) [動画] 東進: 13個 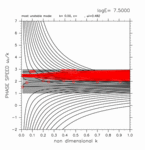西進: 13個 -1.20 < y < +1.00 (grid 数 31) [動画] 東進: 16個 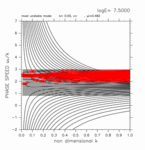西進: 16個 -1.40 < y < +1.00 (grid 数 34) [動画] 東進: 19個 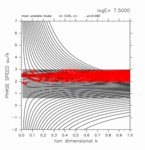西進: 19個 -1.60 < y < +1.00 (grid 数 37) [動画] 東進: 22個 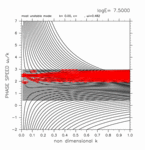西進: 22個 -1.80 < y < +1.00 (grid 数 40) [動画] 東進: 25個 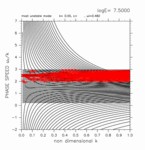西進: 25個 -2.00 < y < +1.00 (grid 数 43) [動画] 東進: 28個 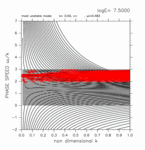西進: 28個

付録 B. 計算領域の南北幅を変えた場合の交差モードの数の変化