本文 3.3 節では, log E=-0.20
の場合の連続モードの構造について記述した.
本節では,
様々な E の値において,
位相速度の値に応じて連続モードの構造がどのように
変化するかを示したアニメーションを列挙する.
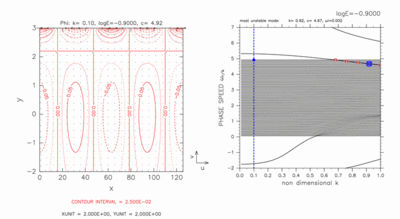
log E=-0.90 の場合の連続モードの構造変化の動画を図A-1 に示す.
位相速度の値に応じた連続モードの構造変化をまとめると
以下のようになる.
- 4.67 ≤ c ≤ 4.92 :
y=3.00 付近に連続モード,
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
- 3.32 ≤ c ≤ 4.59 :
y=3.00 付近に北側境界ケルビン波モード的な構造,
その南側に連続モード,
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
- 2.45 ≤ c ≤ 3.24 :
y=3.00 付近に北側境界ケルビン波モード,
その南側に連続モードの構造が存在する.
振幅は小さいながらも,
y=0.00 付近には赤道ケルビン波モード的な構造も現れているようである.
- 1.37 ≤ c ≤ 2.37 :
y=3.00 付近に北側境界ケルビン波モードの構造が存在する.
振幅は小さいながらも, y=0.80 付近を中心として,
ベクトル場に赤道ロスビー波モード的な渦構造が見える.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- c ≤ 1.30 :
北側境界付近に北側境界ケルビン波モード,
赤道より北側に赤道ロスビー波モード的な構造が存在する
(北側境界ケルビン波モードの構造と重なっているように見える).
振幅は小さいながらも, 赤道より南側に連続モードの構造が存在する.
図A-1: log E=-0.90, k=0.10 の場合の
連続モードの水平構造(左図)と分散曲線上の位置(右図の青丸).
図をクリックすると右図の青点線に沿って連続モードを走査した
動画を見ることができる.
右図中の記号の意味については, 表1 を参照のこと.
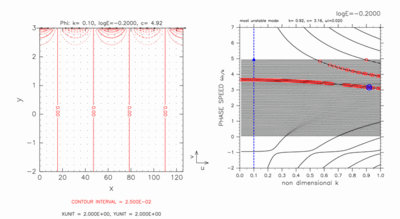
log E=-0.20 の場合の連続モードの構造変化の
動画を図A-2 に示す.
この場合の連続モードの構造変化については,
本文 3.3 節 で記述したので
そちらを参照されたい.
図A-2: 図A-1 と同様の図. ただし, log E=-0.20, k=0.10 の
場合.
ただし, 動画には減衰モード(k=0.10, c=3.65)の図は含めていない.
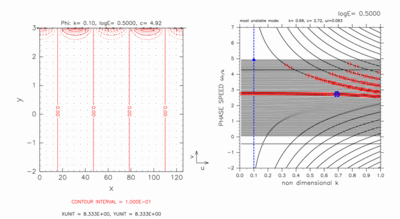
log E=0.50 の場合の連続モードの構造変化の動画を図A-3 に示す.
位相速度の値に応じた連続モードの構造変化をまとめると
以下のようになる.
- 4.76 ≤ c ≤ 4.92 :
y=3.00 付近に連続モードの構造が存在する.
- 4.36 ≤ c ≤ 4.68 :
y=3.00 付近に北側境界ケルビン波モード的な構造,
その南側に連続モードの構造が存在する.
- c=4.30 :
y=3.00 付近に北側境界ケルビン波モードの構造が存在する.
この場合には連続モードの構造を確認することは出来ない.
- 3.80 ≤ c ≤ 4.27 :
y=3.00 付近に北側境界ケルビン波モード,
その南側に連続モードの構造が存在する.
- 3.64 ≤ c ≤ 3.72 :
y=2.00 付近に連続モードの構造が存在する.
- 2.99 ≤ c ≤ 3.56 :
y=1.50 付近に連続モード,
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
- 2.81 ≤ c ≤ 2.90 :
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- c=2.77 :
この位相速度において,
連続モードと赤道ケルビン波モードとの共鳴で不安定が発生する.
動画には不安定モードの構造の図だけが含まれる.
不安定モードでも減衰モード(図は示さない)でも
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
連続モードの構造は陽には見えない.
y=1.20 付近に赤道ロスビー波モード的な構造が存在する.
- 1.72 ≤ c ≤ 2.71 :
y=1.20 付近に赤道ロスビー波モード的な構造,
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- c ≤ 1.64 :
y=1.20 付近に赤道ロスビー波モード的な構造
(c の減少に伴い徐々に小さくなる),
y=0.00 付近に赤道ケルビン波モード的な構造
(c の減少に伴い徐々に小さくなる),
その南側に連続モードの構造
(c の減少に伴い, y=-2.00 に近づいていく)
が存在する.
図A-3: 図A-1 と同様の図. ただし, log E=0.50, k=0.10 の
場合.
ただし, 減衰モード(k=0.10, c=2.77)の図は含めていない.
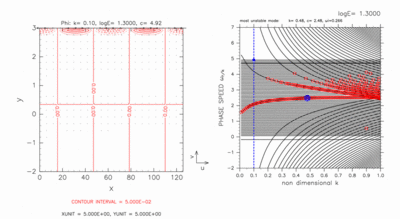
log E=1.30 の場合の連続モードの構造変化の動画を図A-4 に示す.
位相速度の値に応じた連続モードの構造変化をまとめると
以下のようになる.
- 4.84 ≤ c ≤ 4.92 :
y=3.00 付近に連続モードの構造が存在する.
- c=4.76 :
y=3.00 付近に北側境界ケルビン波モード,
その南側に連続モードの構造が存在する.
- c=4.72 :
y=3.00 付近に北側境界ケルビン波モードの構造が存在する.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- c=4.68 :
y=3.00 付近に北側境界ケルビン波モード的な構造,
その南側に連続モードの構造が存在する.
- 4.21 ≤ c ≤ 4.60 :
2.00 ≤ y ≤ 3.00 に連続モードの構造が存在する.
- c=4.19 :
東進混合ロスビー重力波モードの構造が存在する.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- 2.84 ≤ c ≤ 4.13 :
北側に連続モード,
その南側に東進混合ロスビー重力波モード的な構造が存在する.
赤道付近には, c
が大きいうちは振幅は小さいけれども赤道ケルビン波モード的な構造が見られる.
c が小さくなるにつれて,
y=0.00 付近では赤道ケルビン波モード的な構造が顕著になる.
- 2.51 ≤ c ≤ 2.75 :
北側に東進混合ロスビー重力波モード的な構造,
その南側に連続モード,
赤道上に赤道ケルビン波モード的な構造が存在する.
- 2.10 ≤ c ≤ 2.42 :
北側に赤道ロスビー波モード的な構造(振幅は小さい),
その南側に赤道ケルビン波モード的な構造が存在する.
この場合のモードの水平構造の図では,
連続モードの構造を確認することは出来ない.
- c=2.09 :
この位相速度において,
赤道ケルビン波モードと西進混合ロスビー重力波モードの共鳴で不安定が発生する.
動画には不安定モードの構造の図だけを示してあり,
減衰モードの構造の図は含めていない.
不安定モードでも減衰モード(図は示さない)でも
y=0.00 付近に赤道ケルビン波モード的な構造が存在する.
連続モードの構造は陽には見えない.
- 1.40 ≤ c ≤ 2.02 :
北側に赤道ロスビー波モード的な構造,
その南側に赤道ケルビン波モード的な構造が存在する.
連続モードの構造は,
赤道ケルビン波モード的な構造に重なっていて見えないが,
c の減少と共に次第に南側に分離して現れる.
西進混合ロスビー重力波モードの構造も混入している可能性もあるが,
その構造は図では確認することができない.
- c ≤ 1.33 :
この範囲の位相速度では, 連続モードの構造だけが明瞭に見える
(c の減少と共に次第に南下していく).
図A-4: 図A-1 と同様の図. ただし, log E=1.30, k=0.10 の
場合.
ただし, 減衰モード(k=0.10, c=2.09)の図は含めていない.