TI2006 の結果では, 赤道ロスビー波モードが陽に現れなていなかった. 表1 の分散曲線図では 赤道ロスビー波に対応するモードの分散曲線を見出すことができない. ( アニメーション図 も参照). これに関して, TI2006 は, 赤道ロスビー波モードは連続モードに同化している と議論していた. しかし, 赤道ロスビー波モードが連続モードに同化していることを あらわす水平構造の図は示されていなかった. ここでは, TI2006 と全く同様の計算で得られる連続モードの構造を観察し, 赤道ロスビー波的な構造を持つ連続モードが存在していることを確認する. 計算領域として -2.00 ≤ y ≤ 3.00 を考える.
連続モードの水平構造を調査したところ, 赤道ロスビー波的な構造を 持つ連続モードの存在を見出すことができた. その 1 例を図2に示す. 図2 (左) は c=1.48 の位相速度を持つ 連続モードの水平構造を示したものである. このモードの分散曲線図における位置を 図2 (右) の青丸で示してある. 連続モードは, 位相速度と等しい基本場速度を 与える緯度(臨界緯度)で振幅ピークをもつはずであり, 実際に y=-0.52 付近にジオポテンシャルの振幅のピークが存在している. これに加えて, y=1.50 付近にも ジオポテンシャルの振幅のピークが見える. このピークの存在は別のモードの混在を示唆している. 混在しているモードとして, 赤道ロスビー波モード が考えられる. 分散曲線(図2 右)で考えると, このモードの分散曲線は赤道ケルビン波モードの分散曲 線と西進混合ロスビー重力波モードの分散曲線との間に位置し ており, 存在している可能性があるモードとしては 赤道ロスビー波モードしかない. 図2 (左)の y=1.50 付近の構造も赤道ロスビー波の構造と矛盾しない. したがってこのモードは, y=-0.50 付近にピークを持つ連続モードと y=1.50 付近にピークを持つ赤道ロスビー波モードが同化したモードで あると考えられる.
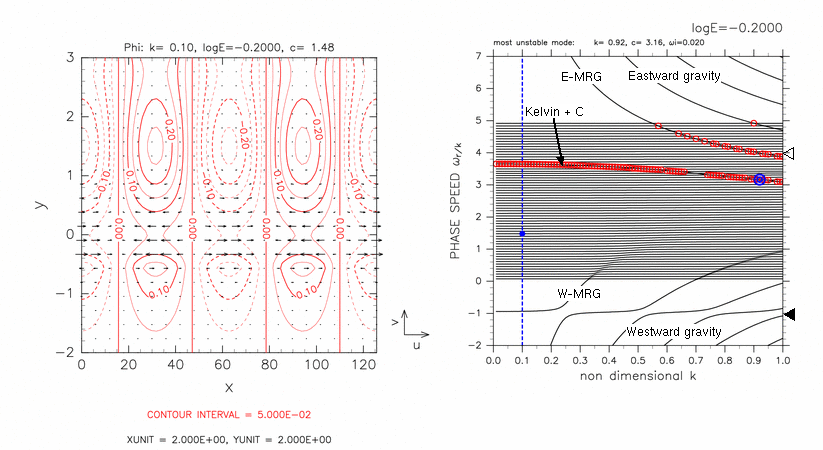
図2: ロスビー波的な構造を持つ連続モード. 左図は log E=-0.20, k=0.10, c=1.48 の連続モードの ジオポテンシャルφ (等値線)と速度場 (u,v; ベ クトル). 等値線間隔は, 5.00 × 10-2. である. 波線は負の値を示す. 右図は log E=-0.20 の場合の分散曲線図. 青●の点は左図の連続モードに対応する点をあらわしている. "Kelvin + C" のラベルは, 赤道ケルビン波モードと連続モードとの共鳴によ る不安定モードを示す. その他の記号の意味については, 表1 を参照のこと.
赤道ロスビー波的な構造を含む連続モードは 0 ≤ c ≤ 2.5 の範囲に存在する. これは連続モードの構造を走査するとわかる. その結果を図3に示す. 連続モードの構造は, 位相速度が変化するに従って図 3 の中の ■, ■ の説明に示すように変化する. 連続モードの位相速度が力学的赤道での基本場の流速値 2.5 よりも 小さい場合 (図3 の ■, ■ で示された領域のうち, 下の3つの領域) ではロスビー波的な構造が 現れる. 図3 には示されていない E の値においても 赤道ロスビー波的な構造を含む連続モードが 存在していることも確認された (付録 A参照).
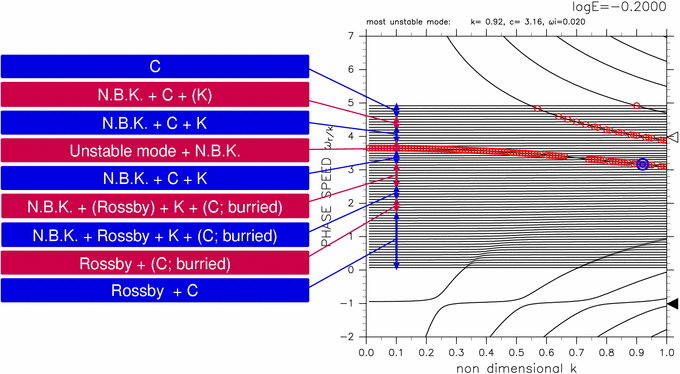
図3: log E=-0.20, k=0.10 の場合における連続モードの 水平構造のまとめ. 右の分散曲線図中の赤矢印, 青矢印で示された 位相速度の範囲におけるそれぞれの連続モードの構造の特徴を 左の ■, ■ に記した. C は連続モード, N.B.K. は北側境界ケルビン波モード, K は赤道ケルビン波モード, Rossby は, 赤道ロスビー波モード, の 構造が現れることを示している. 右図中の記号の意味については, 表1 を参照のこと. 左の■, ■ の部分 をクリックすると 連続モードの水平構造を見ることができる. [動画] をクリックすると, k を固定して連続的に連続モードを走査した アニメーション図を見ることができる.