使用する方程式は, TI2006 と同じプリミティブ系における水平構造方程式に β平面近似を施したものである. 散逸は考えない. 東西方向に無限に伸びる赤道域水路を考える. 南北境界において南北流速を 0 とする. 東西方向に x 軸をとり, 南北方向に y 軸をとる. y 軸は, y=0 が赤道となるようにとる. Dunkerton (1993) と同様に 水平方向に調和展開し, 線形シアー流に対する摂動を考えると 無次元方程式は以下のようになる.
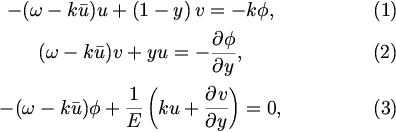
ここで,
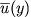 ,
,
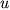 ,
,
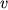 ,
,
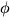 ,
はそれぞれ基本場の流速, 擾乱の東西速度, 南北速度, ジオポテンシャルである.
南北速度
,
はそれぞれ基本場の流速, 擾乱の東西速度, 南北速度, ジオポテンシャルである.
南北速度
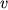 は,
は,
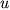 ,
,
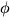 に対して位相を90度ずらして定義してある.
に対して位相を90度ずらして定義してある.
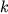 ,
,
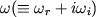 はそれぞれ東西波数, 複素振動数である.
無次元化は, 長さスケール
はそれぞれ東西波数, 複素振動数である.
無次元化は, 長さスケール
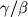 ,
(慣性不安定領域の緯度幅), 時間スケール
,
(慣性不安定領域の緯度幅), 時間スケール
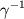 ,
速度スケール
,
速度スケール
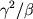 ,
ジオポテンシャルスケール
,
ジオポテンシャルスケール
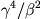 で行った.
ただし,
で行った.
ただし,
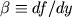 (
(
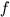 はコリオリパラメータ
),
はコリオリパラメータ
),
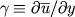 である.
無次元パラメータは,
である.
無次元パラメータは,
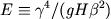 である.
ここで
である.
ここで
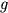 ,
,
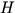 は, それぞれ重力加速度, 等価深度である.
は, それぞれ重力加速度, 等価深度である.
本論で用いる基本場は線形シアー流である. TI2006 と同様に
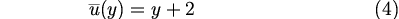
|
を用いる(図1). この基本場では, 慣性不安定領域は 0 ≤ y ≤ 1 (図1の赤斜線領域)となる. TI2006 と同様に, 主に -2 ≤ y ≤ 3 の計算領域を考える. 5 節, 6 節では, 段階的に北側もしくは南側へ計算領域を広げていく場合も考える. 南北方向に方程式系 (1)-(3) を差分化し, 固有値計算を行い不安定 モードを求めた. 南北方向の格子点間隔は 0.078125 である. 擾乱の東西波数として 0.00 ≤ k ≤ 1.00 の範囲を考えた. 計算に用いた E の範囲は, -2.50 ≤ log E ≤ 7.50 である. |
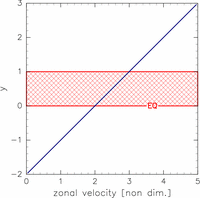
図1: 基本場東西風の南北分布.
横軸は流速
|