TI2006 では, 最低次の東西対称不安定モード (東西波数が 0 のモード) は赤道ケルビン波モードと西向き混合ロスビー重力波モードとの共鳴によって もたらされることが示された (表1). しかし, 高次の東西対称不安定モードをもたらす 中立波の組合せは議論されていなかった. ここでは, TI2006 が示していなかった E の場合についての分散曲線図 を調べることにより, 高次の対称不安定モードがどの中立モード同士の共鳴で 発生しているのかを明らかにする. それによって, Stevens (1983) が得た東西対称不安定モードの 全てに対して, 中立波の共鳴の概念を用いた解釈を 与えることにする. 用いた基本場は TI2006 と同じものである: -2.00 ≤ y ≤ 3.00 (図1).
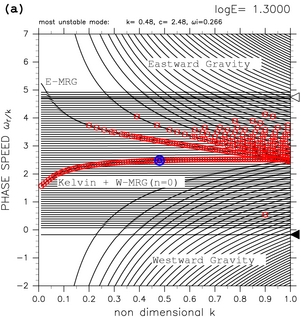
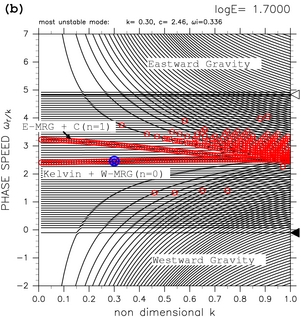
図4 に, log E=1.30, log E=1.70, log E=2.40 の場合の 分散曲線を示す. log E=1.30 (図4a) では k=0 の不安定モードを持つ分散曲線が 1 つだけ存在している (図中では Kelvin + W-MRG (n=0) とラベルされている). この分散曲線上の全てのモードは不安定になっている. これらの不安定モードは, 赤道ケルビン波モードと西進混合ロスビー重力波モード の共鳴により発生している (TI2006). log E=1.70 (図4b) では 東西対称不安定モードを持つ分散曲線が 2 本存在している. 新たに増えた東西対称不安定モードは 東進混合ロスビー重力波モード(E-MRG)と連続モードとの共鳴により 発生している (図中では E-MRG + C (n=1) とラベルされている). log E=2.40 (図4c) では 東西対称な不安定モードがさらに 1 つ増えている. この不安定モードは 最低次の東進慣性重力波モード(E-G)と連続モードとの共鳴により発生している (図中では E-G + C (n=2) とラベルされている). E の増大に伴い 東西対称な不安定モードの数が順次増加していく (図4 の動画). これらの高次モードは, 高次の東進慣性重力波モードと連続モードの共鳴によ り発生する.
 |
 |
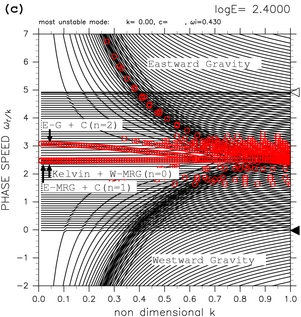 |
図4: 東西対称不安定モードの分散曲線図. (a) log E=1.30, (b) log E=1.70, (c) log E=2.40 の場合. "Kelvin + W-MRG", "E-MRG + C", "E-G + C" のラベルはそれぞれ, 赤道ケルビン波モードと西進混合ロスビー重力波モードの共鳴による不安定モード, 東進混合ロスビー重力波モードと連続モードの共鳴による不安定モード, 東進慣性重力波モードと連続モードの共鳴による不安定モードを示す. これらの図では k=0 のモードの分散曲線は描いていない. 図中の記号の意味は表1と同じ. [動画] をクリックすると E を変化させた時の分散曲線図の変化を見ることができる.
本研究の固有値計算で得られた 東西対称不安定モードの成長率は, Stevens (1983) が得た成長率の式とよく対応している. Stevens (1983) が得た東西対称不安定モードの成長率の式を 本論文の無次元化にしたがって書き下すと次のようになる.
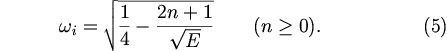
ここで, n は固有関数となるHermite 多項式の次数である. 式(5)から得られる東西対称不安定モードの 成長率を図5の点線で示す. モード番号 n が大きくなるほど, 各モードが 不安定となる E の臨界値も大きくなる. この図には上記の固有値計算で得られた東西対称モード の成長率の計算結果も色で示してある. 不安定が発生する E の臨界値及び E が小さい場合の成長率の値は, 両者でよく一致している. この図から, n=1 の不安定モードは, 上記の固有値計算で得られた 東進混合ロスビー重力波モードと連続モードとの共鳴により 発生する不安定モードに対応していることがわかる. n=2 の不安定モードは, 上記の固有値計算で得られた 最低次の東進慣性重力波モードと連続モードの共鳴によって 発生する不安定モードに対応している.
E→∞ における成長率の漸近値は, 理論値よりも 小さな値を取っている. この誤差は数値計算の解像度による. 高解像度(高格子点数)の計算を行うと, この漸近値は理論値に近付く (図は示さない).
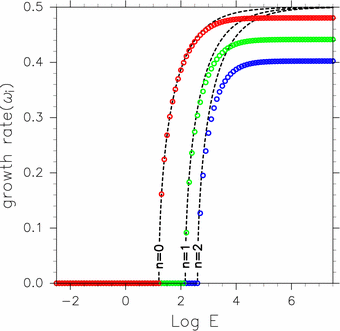
図5: 東西対称不安定モードの成長率の E 依存性. 点線は Stevens (1983) の解析解 (式(5)) から得られた n=0, n=1, n=2 の不安定モードの成長率を示す. 赤, 緑, 青色の◯印は, 固有値計算により得られた東西対称モードの成長率である. 赤◯印は赤道ケルビン波モードと西進混合ロスビー重力波モードの共鳴により発生する 不安定モード, 緑◯印は東進混合ロスビー重力波モード(E-MRG)と連続モードとの共鳴により 発生する不安定モード, 青◯印は最低次の東進慣性重力波モード(E-G)と連続モードとの共鳴により 発生する不安定モードを表している.