Next: A.5.1 線形安定性解析の結果( Ta=0 及び Ta=104 の場合) Up: A 計算の詳細について Previous: A.4.3 渦度と速度の関係
各変数(![]() )を
)を![]() 方向にはFourier級数展開、
方向にはFourier級数展開、![]() 方向にはルジャンドル多項式展開する。
方向にはルジャンドル多項式展開する。
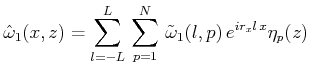 |
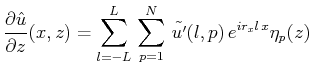 |
||
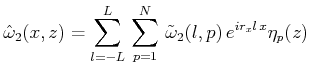 |
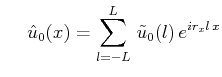 |
||
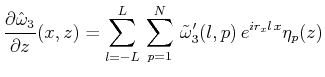 |
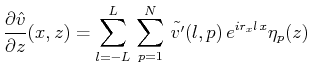 |
||
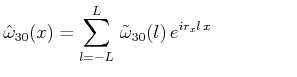 |
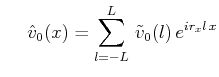 |
||
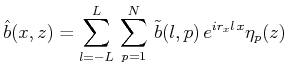 |
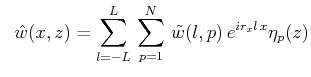 |
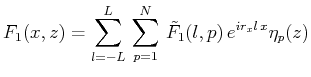 |
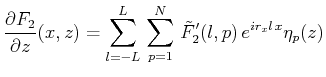 |
||
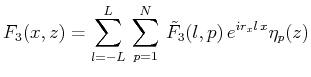 |
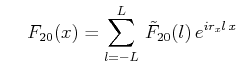 |
![\begin{displaymath}\sigma \left(
\begin{array}{c}
\tilde{\omega }_1(-L,1) \\ [-....
...]
\vdots \\ [-.45em]
\tilde{\omega }_{30}(L)
\end{array}\right)\end{displaymath}](img580.png) |
(56) |
行列Aの成分を求める。まず、![]() とし、他の成分を全て0として
とし、他の成分を全て0として![]() を計算すると、これは行列Aの第1列である。同様にして、行列Aの全ての列が計算できる。
を計算すると、これは行列Aの第1列である。同様にして、行列Aの全ての列が計算できる。
この行列Aの固有値![]() と右固有ベクトルをLAPACKを用いて計算する。
と右固有ベクトルをLAPACKを用いて計算する。![]() の虚部が摂動の発達率に相当している。
の虚部が摂動の発達率に相当している。