| 木星雲対流モデルの開発 | << Prev | Index| Next >> |
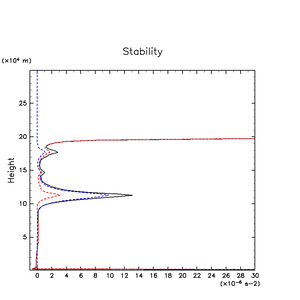
図 3.5 は, 時間水平平均した静的安定度 N2 (浮力振動数 N の自乗) の鉛直分布である. H2O 凝結高度付近に強い極大が存在している. その値は, 鉛直一次元熱力学平衡大気モデルの計算結果(補遺 G参照) に比べて 1/3 程度ではあるものの, H2O 凝結高度が力学的・物質的境界として作用する ( 3.2 節参照) には十分な大きさであったと考えられる. また, 図 3.5 には, N2 に対する 分子量の鉛直勾配の寄与 (凝結性物質混合比の寄与) と温度勾配の寄与 (潜熱による加熱の寄与) とを分割して示してある. H2O 凝結高度付近の N2 の大きさは主に分子量勾配の寄与で決まっており, 温度勾配の寄与は相対的に小さい.
NH4SH 生成高度付近と NH3 凝結高度付近の N2 の値は, H2O 凝結高度付近における値に比べて, それぞれ 1/15, 1/5 倍程度の大きさである. この比率は鉛直一次元熱力学平衡大気モデルの計算結果 (補遺 G参照) で得られたそれぞれ 1/4, 1/3 程度の比率に比べて明らかに小さく, その大きさも 10-6s-1 程度でしかない. その理由は, NH4SH 生成と NH3 凝結高度において, 一次元熱力学平衡計算が予想した様な H2S 蒸気と NH3 蒸気の混合比の急激な減少が生じない (図 3.3 参照) ためである. N2 の値があまり大きくないために, これらの凝結高度は力学的・物質的境界として作用できなかったと考えられる.

図 3.5: 水平・時間平均した静的安定度 N2 の鉛直分布(黒線). 赤線は静的安定度に対する温度勾配の寄与, 青線は分子量勾配の寄与である.
| 木星雲対流モデルの開発 | << Prev | Index| Next >> |