|
γ�Ҳ���ή®¬��ˡ�ȱ���ư���ͥ륮�����Ѥ�����ž����¸���ȯ�����뷹�������Ȥ����̲�
|
<< Prev |
Index|
Next >>
|
����Ͽ1�Ǥϡ��¸�1�ˤ����륹�ԥå״��֤α�ư�Ҥ������������Ȥ�عԤ��������åȤ�ȯ������ޤǤλ����Ѳ�����
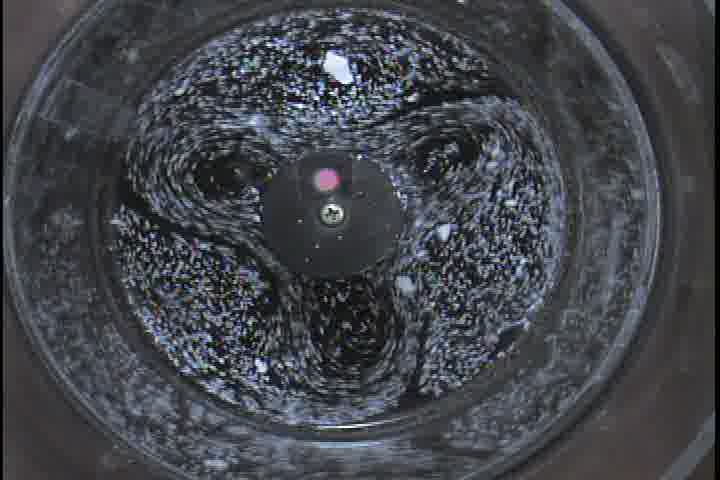
��A1.1�ϡ������Ʊ��®�٤Dz�ž�������ⴶ�٥����ǻ��Ƥ��������Ǥ��롣���������Ȥ�ȯ������ޤǤδ��֤Ρ����̤α�ư���б����������ʴ��ʬ�ۤ��Ѳ�����ǧ�Ǥ��롣
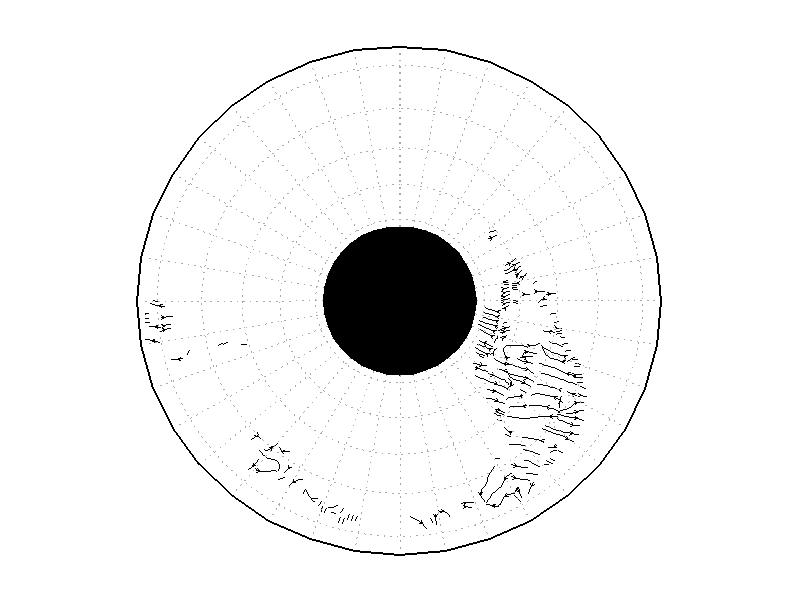
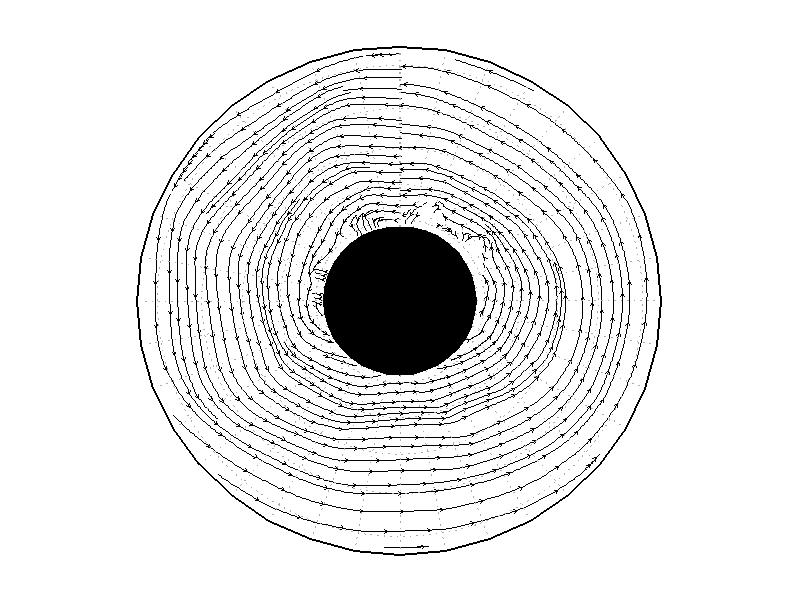
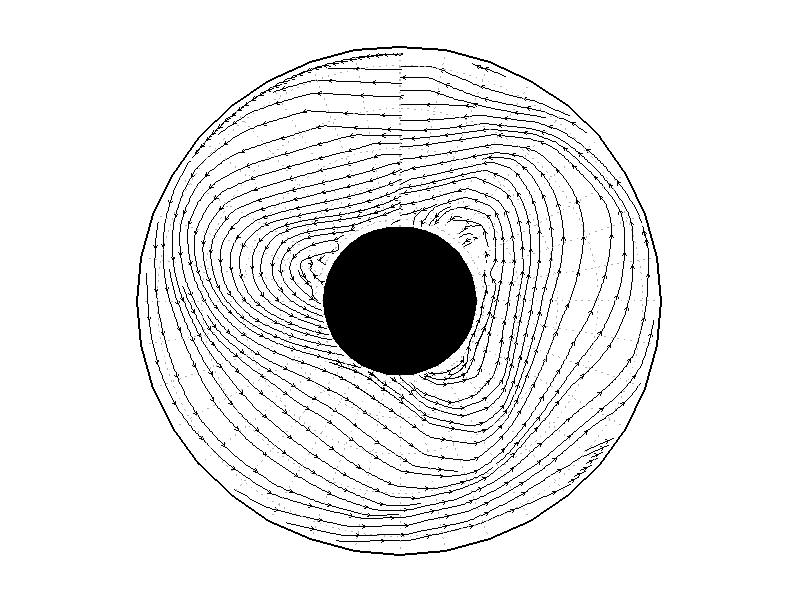
PIV���Ϥ�Ԥ����Ȥˤ�ꡢ���β���������̤α�ư���İ����롣��A1.2����A1.3����A1.4�ϡ���A1.1��Ʊ�����֤�������줿���̤α�ư�٥��ȥ롢®��ʬ�ۡ����б���ʬ�ۤǤ��롣(a)�α��פ���ž���Ƥ��ʤ����֤Ǥϡ����̾�ǤϤۤȤ�ɱ�ư�������Ƥ��ʤ�����������ž�Ϥ���ȡ�������������ˤ�ꡢ¦�ɤ����Ϥ���ü�ο����������ư��Ϥ�롣�Ϥ���Τ�����¦�ɤ���Υ�줿�¸��������ն�Ǥϱ���ư�ϵ����Ƥ��ʤ��ʿ�ά�ˤ���(b)�μ¸����Ϥ�����3ʬ����ȡ��¸��������դ���ơ��¸������Το��̤���ž������Ʊ��������ȿ���ײ��ˤα���ư�롣®�٤ϡ���¦¦�ɤǰ����礭����5.0mms-1����¦¦�ɤ���3.0mms-1���������2.0mms-1�Ǥ��롣���б��پ�Ǥߤ�ȡ�Ⱦ��������®�ٺ����礭���Ȥ��������б��٤��礭������¦������¦����®�ˤʤ��ΰ�Ǥ������١����εդ��ΰ����α��٤�ʬ�ۤ��Ƥ��롣
(c)�μ¸����Ϥ�����4ʬ�塢����ư�Ϥ�����Ϥ�롣3��������6.0mms-1��®�٤��礭���ΰ褬��¦������¦�س��礹�롣���θ��̤Ǥϡ�®�٤ξ������ΰ褬�������ˤΤӤƤ��롣(d)�μ¸����Ϥ���5ʬ30�ø塢��®�٤��ΰ�ϼعԤ��ʤ��飱�ĤˤĤʤ��ꡢ�����åȤ䷹�������Ȥ�ȯ�����롣�¸����Ϥ�����7ʬ�塢�ȿ�3�μعԤ��������åȤι�¤�ϡ����θ���20ʬ���Ѥ�餺�������֤ˤʤä��Ȥ����롣
���������֤˻��ޤǤδ��֡��Ĥޤꥹ�ԥåפλ��֤�������Ū�˰��פ��뤫�ɤ���Ĵ�٤롣��ž�����饨���ޥ�ѥ�ԥ��̤��Ѥꡢ���ο夬���ž������֤Ф���������ȡ����ԥå���T�ϡ�T=2H / (f x He)��H���ؤθ����Ǽ¸�1�ξ��0.02m��f�Υ��ꥪ��ѥ��ϲ�ž®��6rpm�ξ�����0.6s-1�Ǥ��롣He�ϥ����ޥ��ؤθ����ϡ���Ȥ������Ȥ�1�����٤�ͤ��롣�������T=��60s���Ĥޤꡢ������1ʬ�ʾ�ϥ��ԥåפ��פ��뤳�Ȥˤʤ롣�ºݤμ¸��Ǥ���7ʬ�����äƤ��뤬�����������Ȥ��Ƥ������Ȥ����롣
��3.2��ο�3.6�ǾҲ𤷤���ư���ͥ륮���λ����Ѳ��ϡ����ԥå״��֤Ǥ��Ѳ��⼨���Ƥ��롣��ž�����120�äޤ�KE��MKE�����������Ƥ��롣�¸����ϸ夫�餷�Ф餯�ϴ�����������Ư�����¸������ή�Τϱ�ư�ʤ������Τ��ᡢ���Ƥ��줿ư��Ǥϲ�ž�����εո����˱�ư���Ƥ���褦�˸����롣���θ�������ո����α�ư�������뤳�Ȥǡ�KE��MKE���礭���ʤ롣�¸����Ϥ�����3ʬ�����ȡ��¸������Το��̤���ž������Ʊ��������ȿ���ײ��ˤα���ư��Ϥ�뤿�ᡢ���ä��������ȿ�и����α�ư���ܻۤߤޤꡢKE��MKE�ϥ����Ȥʤ롣���θ塢���оݱ�ư����ۤ��뤿��KE��MKE�����ä��롣�����ơ������ø�˷��������Ȥ�ȯ�����뤳�Ȥ�ȼ��EKE�����ä��롣
| (a) |

|
(b) |
 |
| (c) |
 |
(d) |
 |
|
��A1.1:
�ⴶ�٥����ǻ��Ƥ��줿������(a)��ž����30������(b)��ž����200�ø塢(c) 266�ø塢(d)330�ø塣
|
| (a) |
|
(b) |
|
| (c) |
|
(d) |
|
|
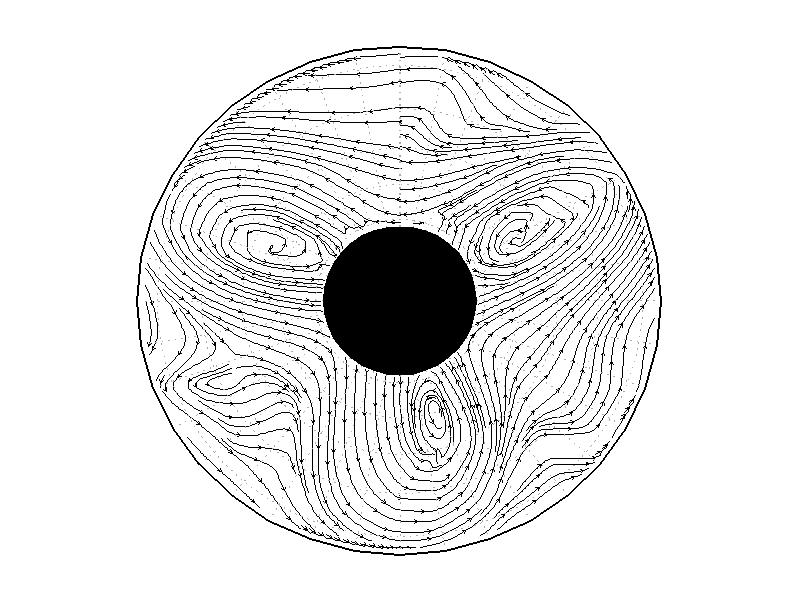
��A1.2:
��A1.1�λ��֤�ή��ʬ�ۡ�
|
| (a) |
|
(b) |
|
| (c) |
|
(d) |
|

|
|
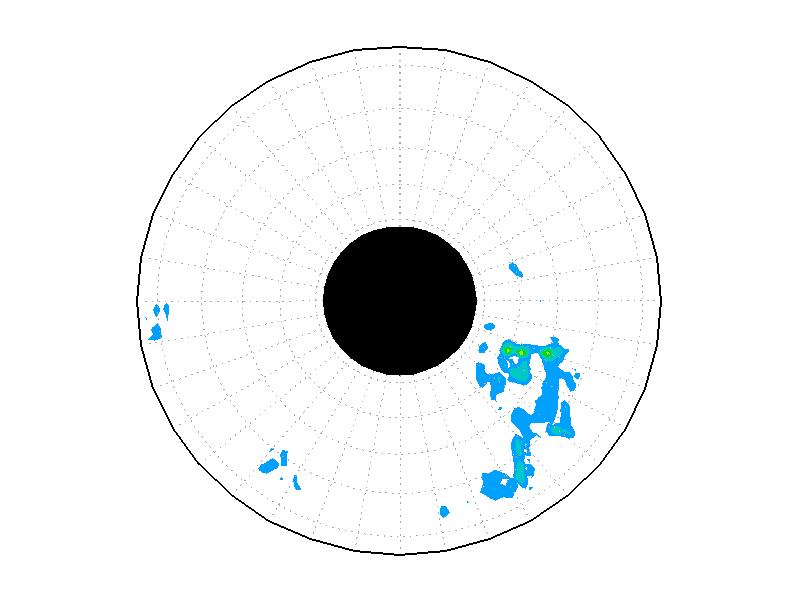
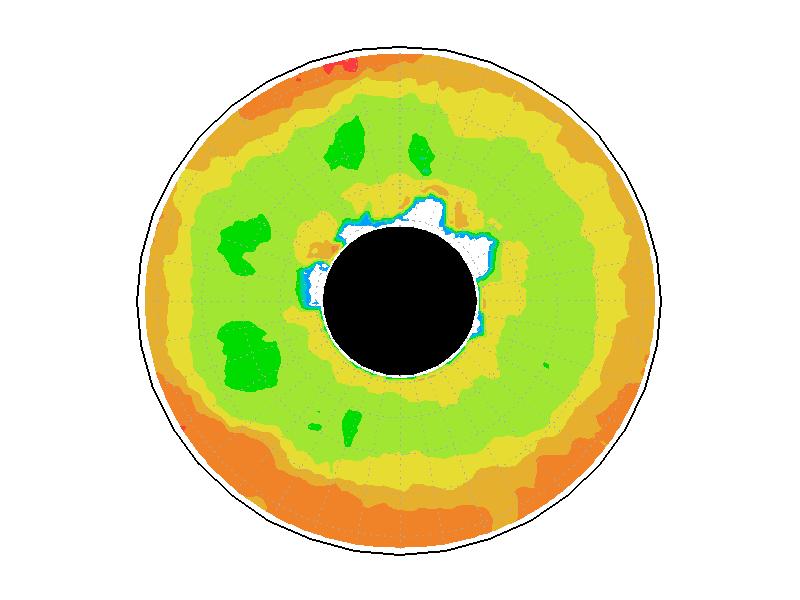
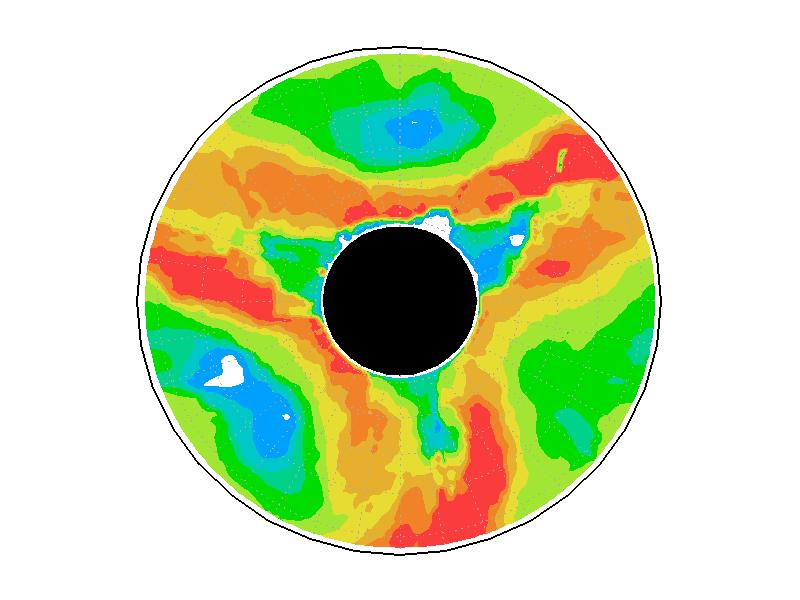
��A1.3:
��A1.1�λ��֤�®��ʬ�ۡ�ñ�̤�mms-1��
|
| (a) |
|
(b) |
|
| (c) |
|
(d) |
|

|
|
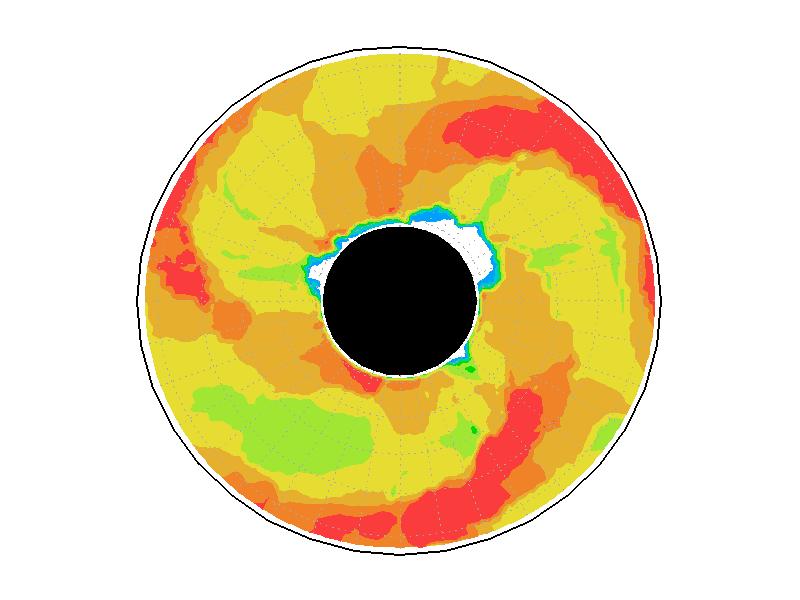
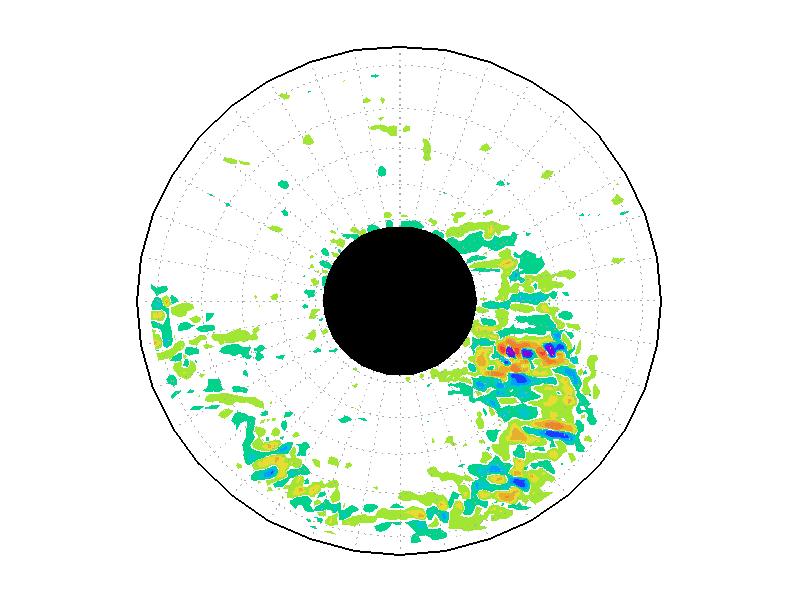
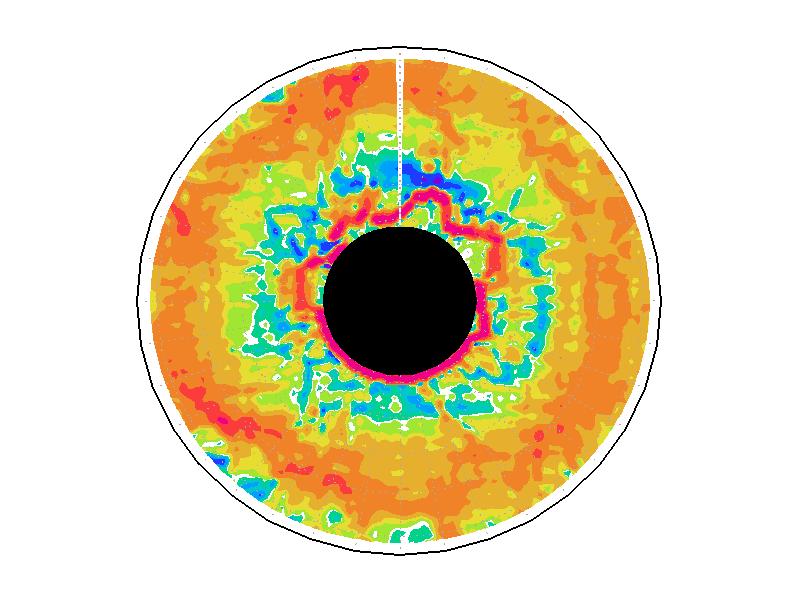
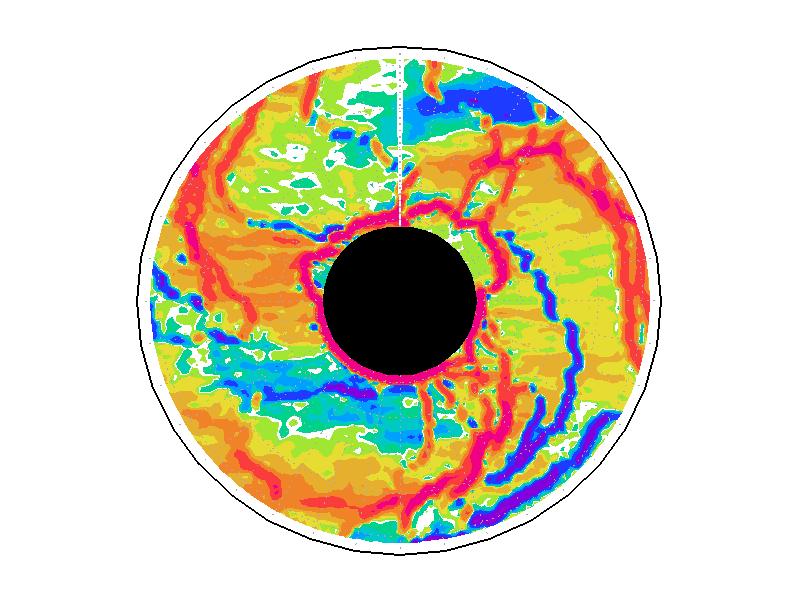
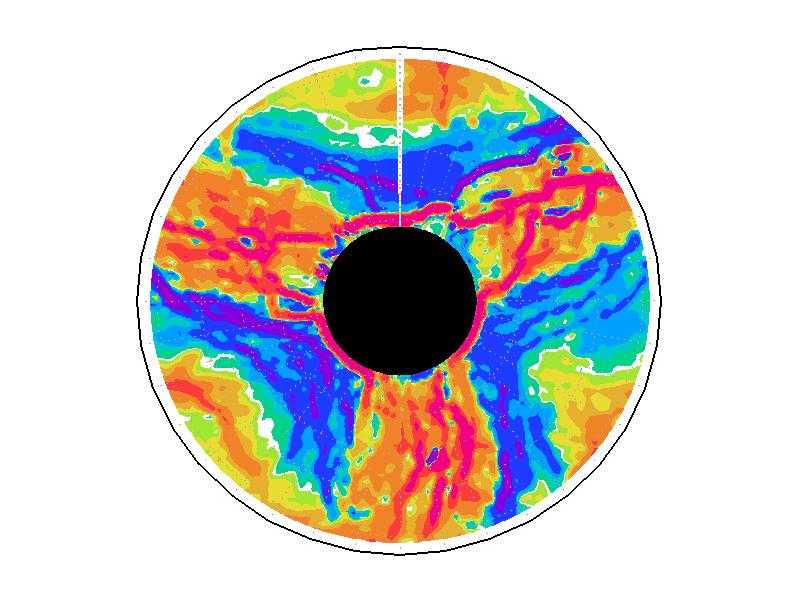
��A1.4:
��A1.1�λ��֤����б���ʬ�ۡ�ñ�̤�s-1��
|
|
γ�Ҳ���ή®¬��ˡ�ȱ���ư���ͥ륮�����Ѥ�����ž����¸���ȯ�����뷹�������Ȥ����̲�
|
<< Prev |
Index|
Next >>
|





















