B. A Summary of One-Dimensional Radiative-Convective Equilibrium Modeling

a. Characteristics of Radiative Equilibrium Solutions: Results of Stratospheric Model

The Stratospheric Model

A stratospheric model similar to those of Komabayashi (1967) and Ingersoll (1969) is considered. Since the solution for the stratosphere is the radiative equilibrium solution, the structure of the stratosphere can be determined by the following three equations:

Here, and represent upward and downward radiative fluxes, respectively, and , where τ is the vertical coordinate. $F^{\uparrow}_{top}$ corresponds to the OLR. Refer to Basic Equations for the definitions of other variables and parameters.

Furthermore, determining equilibrium solution, the lower boundary of the stratosphere is assumed to be saturated. This requirement comes from the assumption that the lower boundary of the stratosphere is equivalent to the tropopause and is situated on the moist adiabatic line. Because q is constant in the stratosphere in the case under consideration, the following relationship holds:

Thus, in this model, the water vapor content is uniquely determined by the value of τ.

Based on the water vapor profile determined by the above equation, the dew point temperature profile is evaluated. This profile is expressed as a function of τ as in the case for the radiative flux formulations. With the use of the definition of, the equation for the saturated water vapor pressure curve

can be rearranged as

Conditions for the Existence of Equilibrium Solutions

If the position of the tropopause is determined, so are the equilibrium solutions in the above model. The tropopause is located at the crossing point of the graphed lines for $\sigma T^{4*}(\tau)$ and the radiation equilibrium solution, . In the figure, the profiles of the radiative fluxes for three representative values for $F^{\uparrow}_{top}$ and the dew point profile, $\sigma T^{4*}(\tau)$ are illustrated.
An examination of this figure leads to the following conclusions:

For W/m²:
Two equilibrium solutions exist. Of the two solutions, the one associated with the higher tropopause does not have a physical meaning since this solution has supersaturated layers within the stratosphere.

For W/m²:
One equilibrium solution exists.

For W/m²:
No equilibrium solutions exist.

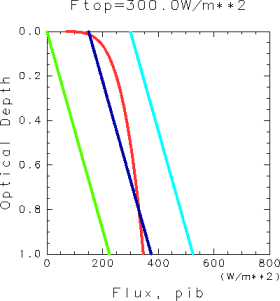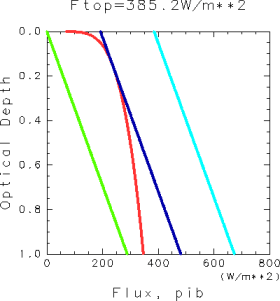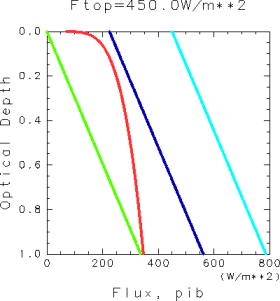
Figure 1: The vertical structures of radiative-equilibrium solutions and the dew point temperature. Red: the values of determined from the dew point temperature, $\sigma T^{4*}(\tau)$ . Aqua: upward radiative flux, . Blue: radiation source function, . Green: downward radiative flux, . The results presented in the figure were obtained for the gravitational acceleration of g = 9.8 m s^-2 and the water vapor absorption coefficient κ of 0.01 m²kg^-1.

According to the above discussions, the following condition needs to be fulfilled for equilibrium solutions to exist in the stratospheric model: There needs to be a crossing point of the graphed lines of $\pi B(\tau)$ and $\sigma T^{\ast 4}(\tau)$ . For the case with the values of the parameters used above, this condition corresponds to
$F^{\uparrow}_{top}$ ≤ 385.2 W/m².

This condition was identified by Komabayashi (1967) and Ingersoll (1969) and will be referred to as the tropopause flux passage condition in the present paper. In addition, the upper limit of the radiation emitted by the atmosphere prescribed by this condition will be referred to as the Komabayashi-Ingersoll limit, as in Nakajima et al. (1992).

B.a. Characteristics of Radiative Equilibrium Solutions: Results of Stratospheric Model