D. 減衰1層の場合の結果

e. 暴走温室状態

S=1800W/m²の場合では, 鉛直層数を 32 とすると最上層にレイリー摩擦・ニュートン冷却をしても長時間積分ができない. その理由は, 鉛直方向に 2-grid noise が生じその振幅が非常に大きくなり最後には CFL 条件を壊してしまうためであるらしい. ここでは, 減衰 1 層のみの計算結果を示しておくことにする.

表面温度・OLR 時間変化

図 1 は表面温度とOLR の全球平均値の時間変化である. この図において 160 日までの結果しか示されていないのは, これより長く計算ができないためである. しかし, OLRは時間とともに減少する傾向にあり, 地表面温度は増加する傾向にある. 160 日しか計算できないにもかかわらずこれでも暴走温室状態が発生しつつあるらしいことは見てとれる.

(a)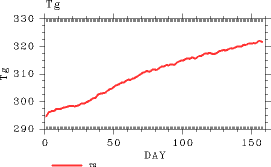

(b) figure1(b)
図 1: 減衰 1 層の大気モデルを用いて得られた S=1800 W/m²の場合における全球平均値の時間変化 (a): 地表面温度(K)の時間変化. (b): OLR (W/m²) の時間変化.

2-grid noise

上で示したように減衰 1 層のモデルで長時間積分が不可能である直接の理由は鉛直方向に2-grid noiseが発生してしまうためであると思われる. このノイズの振幅は上層において時間とともに大きく増大し最後には CFL 条件が壊れてしまい, 最後に積分ができなくなってしまう. その特徴的な例を図 2 に示す. これは赤道付近の一点における u と T の鉛直分布の時間変動を示したものである. 特に u の分布において 2 または 3 点周期の振動パターンが顕著に現れている. T については最上層で温度が極端に上昇する. 以上の特徴は, 対流圏から鉛直伝搬する重力波によってもたらされているものであると想像はされるが, その原因を特定するような解析は全くなされていない.

(a)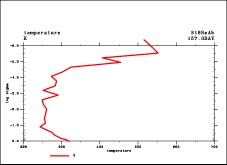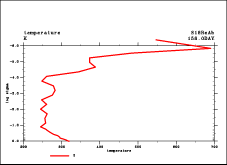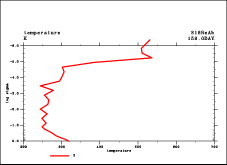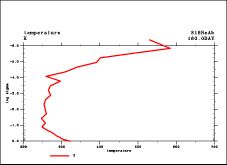

(b) figure2(b)
図 2: 最上層のみにレイリー摩擦・ニュートン冷却を導入した場合の鉛直構造の時間変化. 緯度2.7度上の一点における 157 日目から 160 日までの 3 時間おきの図を動画にしたもの. 太陽定数は S=1800 W/m². 縦軸は logσ でモデル領域全体を示している. (a): 温度(K)の鉛直構造. 横軸の範囲は 200 K から 700 K まで. (b): 東西風(m/sec)の鉛直構造. 横軸の範囲は -200 m/s から 300 m/s まで.

D.e. 暴走温室状態