| 図3 のアニメーションでは、t
= 144 において抽出された
全渦軸を黄色の細線で、代表的な13個の渦芯を色つきの等値面で表したものを
視角を連続的に変えて見ている。
これは、エンストロフィー密度の等値面の複雑さから、乱流が十分に発達した状
態になっていると判断される時刻で、エンストロフィーが最大に達する時刻
のほぼ2倍弱の時間が経過している。
この時刻での乱流レイノルズ数は Rλ= 46
である。
細長い管状の渦構造が、渦軸のまわりに形成されているのが観測できる。
すべての渦芯についてその断面の径の統計をとると、コルモゴロフ長のおおよそ
8倍のまわりに分布している [7]。
これは、別の方法で求められた管状渦の径の大きさと同程度で
ある [9, 10]。
全ての渦芯を同時に描くと、空間を埋め尽くしてしまい、
個々の管状渦が隠れて見えなくなるので、
この図では、任意に選んだ少数個の渦芯のみを表示している。
このような少数個の渦の表示が可能となるのは、
圧力断面極小旋回法では、渦を個別に識別できるからであり、
渦度の等値面表示などではこのようなことができない。 |
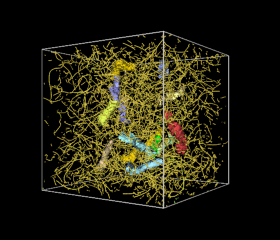 図3: 格子数 1283
の数値計算で実現される渦軸と渦芯 (movie: AVI/
QuickTime) |
