補遺B : 境界条件の差異について 回転系における対流のレジームの遷移と水平スケール：２次元数値計算

境界条件の差異を調べる実験を, 低分解能 Δx =Δz =  0.1 の実験で行なった. この実験における格子配置を 図16 に示す.


図16. 計算領域と格子配置. 格子間隔は Δx =Δz =  0.1 の場合である.

計算は t = 1000 まで行なった.

表1 に t = 1000 における全実験のセル数の変化をまとめた. Rigid-Rigid, Free-Rigid 条件の時, Ra = 104 の場合, Ta = 105, 106 で対流は生じなかった. 理論的には, Ta が大きいほど臨界レイリー数が大きくなり, これらの実験条件は, 対流が発生しない領域にある. 対流が生じる不安定領域では, 一般に レイリーが大きいほどセル数は少なくなる. テイラー数に対する依存性は複雑である. Rigid-Rigid, Free-Rigid 条件のとき, Ra = 104, 105 では テイラー数が大きいほどセル数は多いが, Ra = 106 では逆に減っていく. また, Free-Free 条件では, レイリー数, テイラー数が大きいほどセル数は減る. Rigid-Rigid の場合の Ra = 106, Ta = 106 の実験ははじめに多数のセルがあらわれるが, しだいに消滅して全体に広がる1セルになる. この結果は高分解能の実験の結果と異なっているが, 数値拡散の影響のためと考えられる.

　 　 Ta
　 　 0 10 102 103 104 105 106
Rigid-Rigid Ra = 104 10 10 10 10 12 0 0
Ra = 105 12 10 10 10 18 20 32
Ra = 106 8 8 8 8 8 6 1
Free-Rigid Ra = 104 10 10 10 10 16 0 0
Ra = 105 6 6 6 8 10 24 34
Ra = 106 9 5 7 8 5 1 1
Free-Free Ra = 104 10 10 6 1 1 0 0
Ra = 105 6 6 4 1 1 1 36
Ra = 106 2 2 2 1 1 1 1

表1. 低分解能実験の最終状態 (t = 1000) におけるセル数の一覧.

表中でセル数が1と表示した実験では, 時間的にセル数が減少している. その一例として, Free-Free 条件の Ra = 105, Ta = 103 の実験結果を 図17 に示す. また, z = 0.45 における 温度及び上端, 下端のヌッセルト数の時間変化を 図18 , 図19 に示す. 始めセル数は4だったのが, t = 260 の時点でセルが合体し, 2つになり, さらに t = 680でセル数は１になった. セル数の変化に対応して, ヌッセルト数も大きく変動していることがわかる. セルが合体するときにはヌッセルト数は小さくなる.




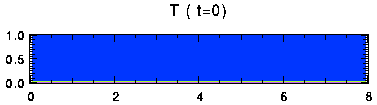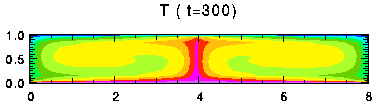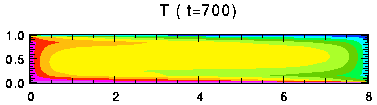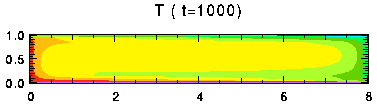
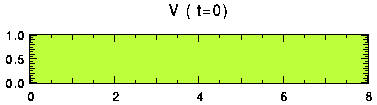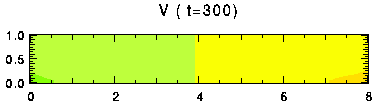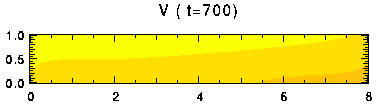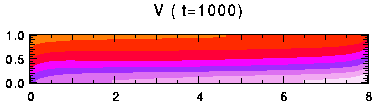
図17. 計算例. Free-Free 条件における Ra = 105, Ta = 103 のときの 温度, 流線関数, v の分布. クリックすると時間変化があらわれる. 色の階調の間隔はそれぞれ, 0.1, 0.2, 2.0.


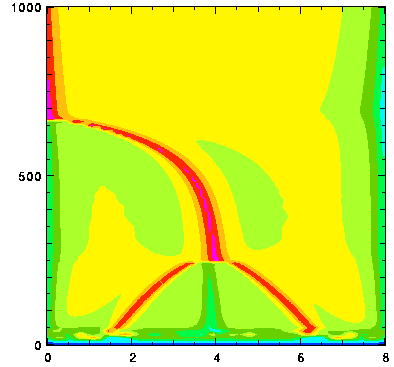
図18. 計算例. Free-Free 条件における Ra = 105, Ta = 103 のときの y = 0.45 における温度分布の時間変化. 色の階調の間隔は 0.1.


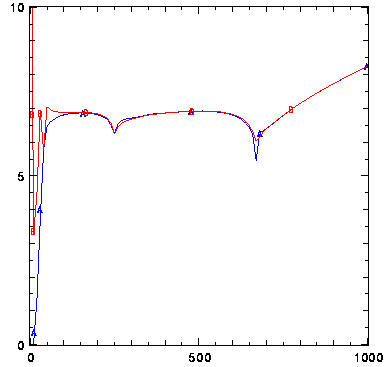
図19. 計算例. Free-Free 条件における Ra = 105, Ta = 103 のときの ヌッセルト数の時間変化. A は最下端( y = 0 ), B は最上端( y = 1 ) における値.

補遺A では スリップ条件での線型論の結果を得た. 臨界波数は (46) 式で, 水平スケールは (1) 式で与えられる. 非線型計算によると, 積分開始直後は線型論に対応して多くのセルが現れるが, しだいにセルは合体し, 系全体まで広がろうとする傾向にある. 一般には両側とも粘着条件であるよりも 片側がスリップ条件の方が水平スケールは広がる傾向にあり, また両側ともスリップ条件を課すとさらに水平スケールは広がる傾向にある. このように, 水平スケールは 境界条件によって異なる結果が得られることがわかる.

補遺B : 境界条件の差異について 回転系における対流のレジームの遷移と水平スケール：２次元数値計算