| はじめに (2) |
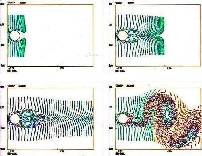
さて,式(3)が解ければ,その解から流線,表面流線,流跡線,タイムライン,統合流脈面等を得ることができる。 これらの方法を通常法と呼ぶこととする。 通常法は実験結果との比較を考える上でも重要である。 また,流跡線,タイムライン,統合流脈面は非定常解をより直感的に捉えるためには優れた方法であり,しばしば動画化が行われる。 図1に円柱を過ぎるレイノルズ数1000の流れに対するタイムラインによる可視化例を示す。 しかしながら,この方法では,すべての粒子が同じように表現されるため,必ずしも流れ場の特徴が抽出しやすいわけではない。 また,通常法による可視化の多くが,表面流線,格子面流線を除き,空間の全領域を表示対象とするため情報量が非常に大きくなることも問題である。 複雑な現象を捉えるには数多くの粒子を必要とすることが多く,特に,三次元空間における可視化結果を把握するための努力は計り知れないものとなる。 そこで,ベクトル場の特徴を容易に把握するための可視化手法を考察する。 式(3)は,特異点とそのまわりの線形化されたベクトル場の表現という解析的な方法によって近似的に解くこともできる。 特異点,特異線探索と局所的線形化によるベクトル場の表現は,多自由度離散系の低次元化による解の近似法と見なすことができる。 一方,可視化情報という観点からは情報圧縮の方法と考えることができる。 ここでは,情報圧縮という面に着目する。
特異点,特異線(限界流線など)と位相幾何的な表示[3,4]が流れ場を可視化する方法として優れていることは,通常法で複雑なパターンとして示された流れ場がいくつかの特異点と特異線によって表現されることから確かめられる。 しかし,線形化の影響[2],抽象的な表現に起因する流れ場の詳細な把握の難しさという問題が生じる。 特に大域的な視点から局所的な部分に注視点を変更する場合,また,逆の場合において,連続して流れ場を認識することが難しい。 このためベクトル図と特異点表示の併用といった方法がとられることが多く,一般的には単独で用いられる可視化法ではないと言える。 しかしながら, 特異点とそのまわりの線形化されたベクトル場の表現が有する情報圧縮という概念が粒子追跡法において重要な意味をもつことには留意し続ける必要がある。
![]()