数値計算 (1) -パラメータ

鉛直切断した系による線形解析によって得られた対流の性質がどの程度まで正しいのかを確かめるために, 支配方程式および境界条件を差分化して時間積分を行なってみた. 計算領域は水平方向に 8 ,鉛直方向に1 であり, 水平方向に 256 点, 鉛直方向に 32 点のグリッドポイントを配置した. 水平方向の境界条件は周期的にしてある. 時間積分は 4 次の Runge-Kutta スキーム, 非線形項は Arakawa のヤコビアンスキームを用いている. 熱伝導解に対して x =4, z =1/4 に振幅 0.01 の温度擾乱をおいたものを初期値として時間積分を実行した.

プラントル数 P = 1, η = 1000 で固定し, レイリー数は (a) R = 10000 と (b) R = 8000 の 2 つの場合について行った. レイリー数が小さいケースでは低波数での不安定領域しかないが, 大きいレイリー数では高波数の不安定領域も存在している.

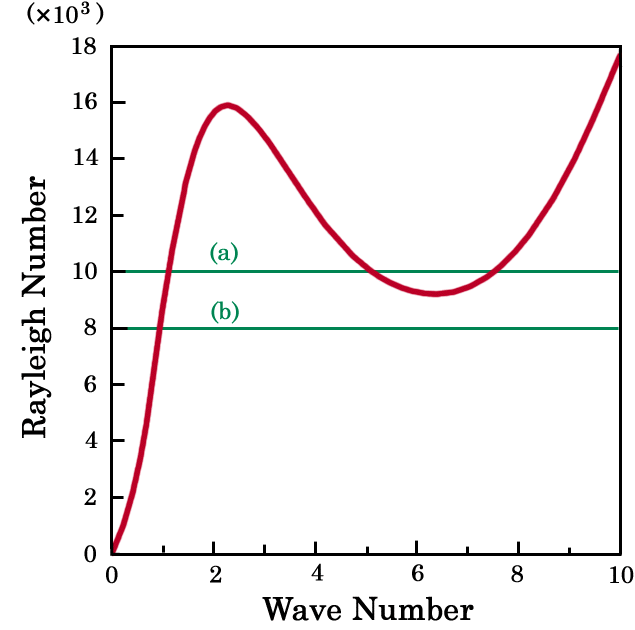図5 数値実験を行ったレイリー数