|
A.d.iii. Radiative transfer of dust
|
The absorption, scattering and emission of solar and infrared
radiation associated with dust are calculated by using the
δ-Eddington approximation (cf., Liou, 1980).
The δ-Eddington approximation is widely used to calculate radiative
transfer with anisotropic scattering.
The asymmetry factor of dust for solar and infrared radiation is
between 0 and 1, which implies that forward scattering occurs.
(see Appendix A.d.v ).
The upward and downward diffuse solar radiative flux per unit wave length
associated with dust
(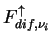 , , 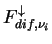 ) are obtained by using the following equations. ) are obtained by using the following equations.
The boundary conditions for Equations (A.31)
and (A.32) are
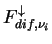 = 0 at the top of the atmosphere and = 0 at the top of the atmosphere and
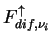 = =
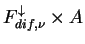 at the surface, where at the surface, where 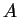 is the surface albedo. is the surface albedo.
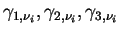 are expressed as follows. are expressed as follows.
where 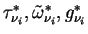 are optical depth, single scattering
albedo and the asymmetry factor modified by the δ-Eddington
approximation, which are given as follows. are optical depth, single scattering
albedo and the asymmetry factor modified by the δ-Eddington
approximation, which are given as follows.
where 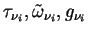 are the optical depth, single scattering albedo and asymmetry factor, respectively.
are the optical depth, single scattering albedo and asymmetry factor, respectively.
The upward and downward infrared radiative fluxes per unit wave length
associated with dust are obtained as solutions of similar equations
that are used to calculate diffuse solar flux
(Equations (A.31) and (A.32)), except that the
single scattering of direct solar radiation term is replaced by the
thermal emission term.
The boundary conditions for Equations (A.33) and
(A.34) are
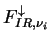 = 0 at the top of the atmosphere and = 0 at the top of the atmosphere and
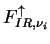 = =
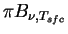 at the surface.
The Plank function at the surface.
The Plank function
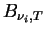 in Equations (A.33) and
(A.34) is averaged over the band width. in Equations (A.33) and
(A.34) is averaged over the band width.
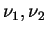 are the lower and upper wave length of the band. are the lower and upper wave length of the band.
The radiative heating rate associated with dust is calculated as follows.
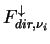 is the direct solar radiative flux, is the direct solar radiative flux,
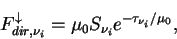 |
(A.37) |
The band width and optical parameters of dust (extinction efficiency, single
scattering albedo, asymmetry factor) for each band
are same as those
of Forget et al. (1999),
excluding the 11.6-20 μm band that are not considered in our model for
computational simplicity.
The overlap of the dust solar band and the CO2 near
infrared band is not taken into consideration.
The effect of this simplification can be negligible
because the total radiative flux absorbed by
CO2 in the near infrared band is 1 % of the incident
solar radiative flux at the top of the atmosphere.
The extinction efficiency for solar radiation (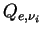 ) is 3.04, which is the
same value for the 0.67 μm solar radiation presented by
Ockert-Bell, et al. (1997).
The visible to infrared opacity ratio is set to 2
(Forget, 1998).
Detailed descriptions of band width and the optical parameters of dust
are provided in Appendix A.d.v. ) is 3.04, which is the
same value for the 0.67 μm solar radiation presented by
Ockert-Bell, et al. (1997).
The visible to infrared opacity ratio is set to 2
(Forget, 1998).
Detailed descriptions of band width and the optical parameters of dust
are provided in Appendix A.d.v.
Dust opacity is calculated by using the mass mixing ratio and
effective radius of dust (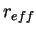 ).
The effective radius is calculated by using the size distribution
function of a dust particle (see Appendix A.d.iv).
In our model, we assume the size distribution of a dust particle is
the modified gamma distribution (Toon et al., 1977). ).
The effective radius is calculated by using the size distribution
function of a dust particle (see Appendix A.d.iv).
In our model, we assume the size distribution of a dust particle is
the modified gamma distribution (Toon et al., 1977).
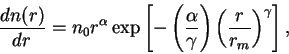 |
(A.38) |
where
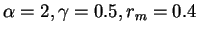 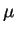 m.
By using these parameters, the effective radius is obtained as
2.5 μm (Pollack et al., 1979). m.
By using these parameters, the effective radius is obtained as
2.5 μm (Pollack et al., 1979).
|