|
支配方程式は 2 次元ブシネスク流体の方程式系に
境界面の地形性β効果を加えたものである(Busse 1986).
| |
|
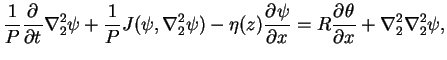 |
(1) |
| |
|
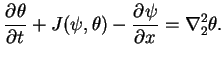 |
(2) |
ただし,
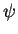 は流線関数, は流線関数,
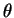 は
基本場に対する温度擾乱である.
P はプランドル数であり, 動粘性率と熱拡散率の比を表す.
R は成層不安定度を表すレイリー数である.
ηは地形性β効果をあらわすパラメターである.
J(A,B) はヤコビアンであり, 渦度と熱の移流を表している.
長さは流体層の厚さで, 時間は熱拡散時間で,
温度は上下面の温度差で無次元化している. は
基本場に対する温度擾乱である.
P はプランドル数であり, 動粘性率と熱拡散率の比を表す.
R は成層不安定度を表すレイリー数である.
ηは地形性β効果をあらわすパラメターである.
J(A,B) はヤコビアンであり, 渦度と熱の移流を表している.
長さは流体層の厚さで, 時間は熱拡散時間で,
温度は上下面の温度差で無次元化している.
地形性β効果を表す項は球の形状を想定して次のような形を用いる
(付録: 支配方程式詳細).
![\begin{displaymath}
\eta(z) = \frac{2s(z)}{E[r_o^2 -s(z)^2]}, \quad
s(z) = s_0 + (s_1-s_0)z
\end{displaymath}](topobeta.gif) |
(3) |
ただし
s0, s1 は
円筒モデルで扱う領域の回転軸からの距離,
ro は外球の半径を表している.
これまでの回転球殻対流の研究では内外半径比 0.4 程度の状況が
よく考察されているので,
我々の計算においては r0=1,
s0=0.4, s1=0.9 なる値を用いた.
熱的境界条件は, 流体層の上面 (z=1), 下面 (z=0) で
温度固定条件を与える.
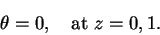 |
(4) |
運動学的,力学的境界条件は,
境界を突き抜けない条件と Free-slip 条件を与える.
![\begin{displaymath}
\psi = \DP[2]{\psi}{z}=0, \quad \mbox{at} \quad z=0,1.
\end{displaymath}](psibc.gif) |
(5) |
水平方向には周期的条件を与える.
|