序論

back top next

1. 序論

　
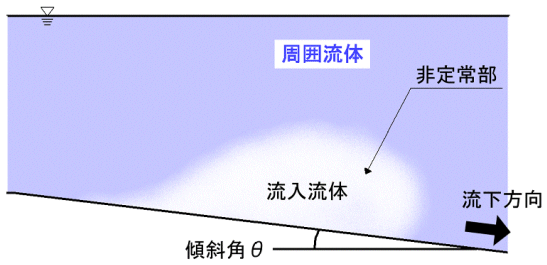図－１　傾斜サーマルの模式図

周囲流体より密度の大きい流体が，斜面上を壁面に沿って流下する現象を傾斜壁面密度流と呼ぶ．さらに上流から流体の供給が定常的にある傾斜壁面プルーム（以下では傾斜プルームと呼ぶ），流体の供給が連続的ではない傾斜壁面サーマル（以下では傾斜サーマルと呼ぶ）とに分類される．一方，密度差の原因となる物質が塩分や温度差のように保存性物質の場合と沈降性の濁質粒子の場合などの非保存性物質の場合にとに分類され，それぞれ，保存性傾斜密度流，非保存性傾斜密度流と呼ばれる．保存性の傾斜プルームは，海水が河口から流入する場合（非定常塩水くさびなど）などに見られる．非保存性の傾斜プルームの代表例は，海底や大規模な湖沼で発生する泥水流などである．上流からの流体の供給が不連続的である傾斜サーマルも自然界で多く観測される．代表例としては，冬季山岳地帯で発生する煙型雪崩，火山の噴火に伴う火砕流などがあり，泥水流には傾斜サーマルの流動形態をとるものも予想されている．これらは何れも作業流体が粒子流で構成される，非保存性傾斜サーマルである．　　

このように傾斜プルームや傾斜サーマルは，自然現象とも密接に関わっている．したがって，自然災害などにかかわる流体現象を解明するためにも，また，傾斜密度流，特にフロントを伴う密度流の基礎的特性を明らかにするためにも，これらの流れの流動機構を解明することが重要といえる．

傾斜サーマルの模式図を図－１に示す．傾斜サーマルは上端部より流入した流体が全体として，非定常なフロント部を形成しながら流下する．このフロント部は大規模な渦運動を伴い複雑な流動機構を示す．本研究の主たる目的は，この傾斜壁面サーマルの流動特性を数値解析により明らかにすることである．傾斜サーマルとして密度差を生ずる原因物質が溶解性の保存性の場合と粒子混合流体で構成される非保存性の場合を対象とする．また，傾斜サーマルでは当然密度変化を伴う．このため，数値解析で用いる乱流モデルの選択にあたっては，保存性及び非保存性の両者の解析が可能であること，密度変化に伴う成層の効果を考慮できるモデルであること，非定常計算が必要となるから，できるだけ単純なモデルであることなどが考慮された．現在，数多くの乱流モデルが提案されているが，以上の観点から本研究ではモデル構成が単純でなおかつ密度成層の効果を表現できるk -ε 乱流モデルを用いることとした．

この研究の前段階として著者らはサーマルモデルという一次元の積分型モデルを基に，煙型雪崩や火砕流のシミュレーションモデルを構築し，その妥当性を検討してきた．いわゆるボックスモデル型のサーマルモデルそのものは，モデルの構成が簡単であるから，現地の複雑な地形変化も考慮しやすいし，計算時間も極めて少ないという長所を有する．その反面，モデル自身に空気の連行係数やサーマルフロントに働く抗力係数，底面や界面に働く摩擦係数を含むことになる．モデル自身の普遍性の点でも，シミュレーションモデルの適用性の観点からもこれらのパラメータの値をどのように決まるかが最大の問題となる．

本研究はこのサーマルモデルの限界を打破するために着手した．積分型のモデルを用いないで，微分型の基礎方程式に基づいた解析を行うことで，様々のパラメータがモデル中に含まれることを避けることができるからである．その一方で，このような基礎方程式を用いた解析が，煙型雪崩や火砕流のようにそれを構成する粒子が斜面上の粒子層とのやり取りをする（底面からの粒子の巻上げと底面への粒子の沈降）ような現象を再現できるか，非定常なフロントの計算が少ない計算時間で実行でき，シミュレーションといった段階まで発展可能か，という基本的な問題を含んでいることも確かであった．

本研究は以上のような問題認識と目標をもって，煙型雪崩や火砕流のシミュレーションの高度を目指して，最も単純な一様勾配斜面での保存性と非保存性の傾斜サーマルの流動解析を行い，これまでに行った室内実験の結果と比較したものである．

back top next