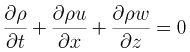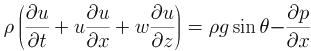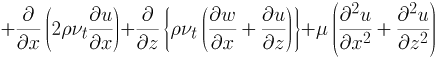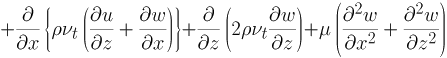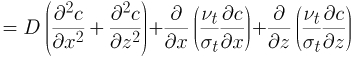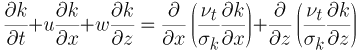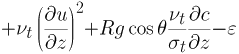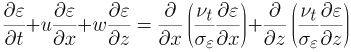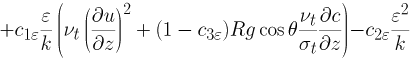2. 理論
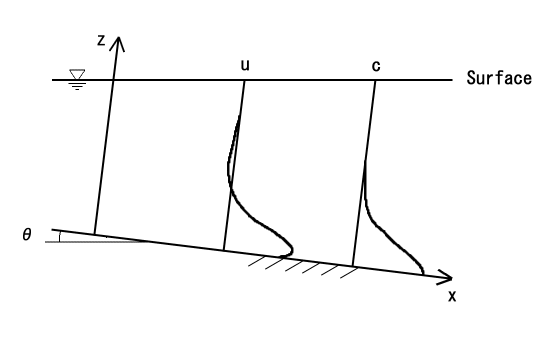 |
| 図−2 傾斜サーマルの計算に用いた座標系 |
傾斜面上での傾斜壁面サーマルの流動を解析するため,図−2に示すような座標系における流れを考える.傾斜サーマルは一定の傾斜角θ をもつ二次元の斜面上に,一様な密度ρw をもつ淡水が満たされ,その中に平均濃度c ,密度ρ の流入流体(以下で比較しているのは,塩水あるいは硫酸バリウム混合水)が置かれることによって発生するものとする.流れは,本質的に非定常で,十分に発達した乱流である.流入流体によって生じる密度差をΔρ とし,塩分または硫酸バリウム粒子などの密度差の原因となる物質の輸送は乱流拡散方程式で記述できるものと考える.乱流運動に基づく渦動粘性係数,渦拡散係数は場所ごとに変化するが,これらの値は方向に依らず,流下方向x と上向き方向z で等しいと考える.時間をt で表す.u ,w をx 方向とz 方向の平均流速成分,p を平均圧力,乱れ運動エネルギーをk ,分子粘性消散率をε ,重力加速度をg で表す.
このとき,連続式,流下方向と斜面と直交方向のレイノルズ方程式,密度差の原因物質の輸送方程式,乱れ運動エネルギーk の方程式,分子粘性消散率ε の方程式は次のように表される.用いたのは標準型のk
-ε乱流モデルである.
■ 連続式
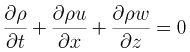 |
(1) |
■ x方向運動量方程式
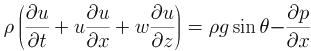 |
|
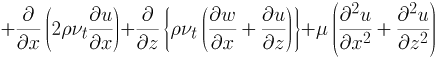 |
(2) |
■ z方向運動量方程式
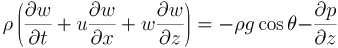 |
|
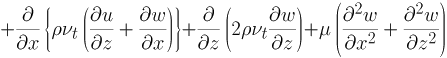 |
(3) |
■ 拡散方程式
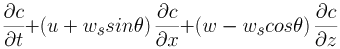 |
|
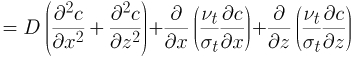 |
(4) |
■ 乱流運動エネルギーk の方程式
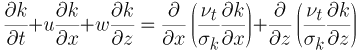 |
|
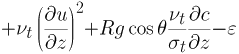 |
(5) |
■ 分子粘性逸散率εの方程式
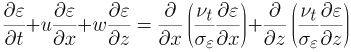 |
|
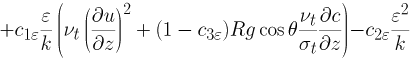 |
(6) |
ここで,νtは渦動粘性係数であり,k とε を用いて次のように表す.
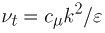 |
(7) |
ここで,μ は水の粘性係数,D は塩分の分子拡散係数である.また,σt ,σk ,σε ,cμ ,c1ε ,c2ε ,c3ε はk -ε 乱流モデルの数値定数である.Rc = (ρs - ρw ) / ρw は淡水中での密度差原因物質による相対密度差(R は定数)である.数値計算に用いた数値定数の値を表−1にまとめて示す.ここで,ρs は流入水の初期密度である.
偏微分方程式の離散化にはPatankar(1985)が提案しているSIMPLE法を用いた.これは移流拡散流束に対する独自の離散化手法を用い,スタッガード格子を導入し,さらに圧力方程式を解くものである.
| 表−1 数値計算に用いた数値定数 |
 |