| back | top | next |
2. 理論
| 2. 2 境界条件 |
(a) 底面境界条件
今,流入流体と周囲流体との密度差は十分小さい場合を考えている.そこで,壁面での境界条件として,一様流体に対して得られた,壁関数法をそのまま用いた.煙型雪崩や火砕流では密度差が極めて大きくなる場合もあり,壁面での境界条件としてどのような形を用いるかについては留意もひつようであろう.壁関数法が成り立つすれば,流速分布は次のように対数則を用いて表される.ただし,壁面は滑面であると仮定している.壁面からz0 だけ離れた点をz = z0 とするときu は,
| (8) |
となる.ここで,u* は摩擦速度,κ はカルマン定数,ν は動粘性係数(= μ / ρ ),As = 5.5 である.境界近傍の2点でこの式(8)が成り立つものとして,u* をニュートン法による繰り返し計算で求め,境界近傍でのu を算出した.壁関数法ではw,k,ε は次のように与えられる.
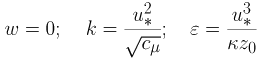 |
(9) |
濃度c に対する底面境界条件は,塩水サーマルに対しては塩分フラックスが固定面上で零となるので次の境界条件が成り立つ.
| (10) |
粒子サーマルに対しては濃度勾配を規定することとし,次式を用いる.
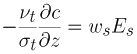 |
(11) |
ここでEs は粒子の連行係数であり,Es の関数形の一例としてはたとえば,以下のGarcia(1990)の提案式がある.
| (12) |
ここで,Z は次のように与えられる.
| (13) |
ここでA = 1.3 × 10-7 ,Ds は粒子の粒径,Rp は粒子レイノルズ数である.この式は河川における浮遊土砂流に関する実験結果を整理したもので,水流において粒子の密度が水の密度に比べてそれほど大きくなる場合に適用可能である.
(b) 上部境界条件
上部境界z = H(x) は水面(自由水表面)である.ここでは,流速に対しては水面が流線であること,水面でせん断応力が零になることの2つの条件を与えた.乱れ運動エネルギーk と分子粘性逸散率ε は水面との直行方向の勾配が零になるものとした.
(c) 上流端境界条件
上流端は固定壁面であるとし,底面の境界条件と同様な境界条件を与えた.
(c) 流出部境界条件
流出部ではu,w,c,k,ε の流下方向の勾配が零になるものとして,次のように与えた.
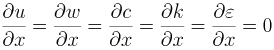 |
(14) |
| back | top | next |