4.2.1 結果

3.2節のa.の時間発展のデータから、順圧平均流成分・順圧渦成分・傾圧成分それぞれの運動エネルギーの時間変化を求めたものを図5に示す。また、順圧平均流成分・傾圧成分から順圧渦成分へのエネルギー変換の時間変化も図6に示す。

図5より、ロール状対流が発達し始める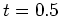頃に順圧平均流成分と傾圧成分が増加する。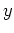方向波数4,5の擾乱が現れてロールが壊れ始める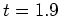頃に順圧平均流成分が急激に減少、傾圧成分も減少、順圧渦成分が増加し始める。波数1成分の擾乱が大きく発達する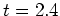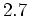～頃、順圧渦成分が著しく増加して順圧平均流成分が同程度減少する。それ以降、順圧渦・順圧平均流成分が反対称に振動する。

順圧渦成分へのエネルギー変換を示した図6より、ロールが壊れ始める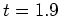以降に傾圧成分からの変換が存在するが、波数1成分の擾乱が大きくなる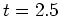頃に順圧平均流成分からの非常に大きなエネルギー変換が存在する。この図だと、傾圧成分から順圧渦成分への寄与も大きく見えるが、順圧波数1成分への変換に限定した図7を見ると、順圧波数1成分の発達には順圧平均流からのエネルギー変換が主に寄与していることが確認できる。よって、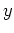方向の波数1成分の擾乱は順圧不安定により発達したのではないかと考えられる。

**図5:** 順圧平均流・順圧渦・傾圧各成分の運動エネルギーの時間変化。各成分に対応する線種については図の上部に示してある。ここに、Barotropic Zonal が順圧平均流、Barotropic Wave が順圧渦、Baroclinic が傾圧、をそれぞれ表す。なお、順圧平均流成分については左側の目盛を、順圧渦・傾圧成分については右側の目盛を読むこと。
$\begin{figure}\includegraphics[trim=15 8 0 20,clip,scale=0.62]{img/energy/energy.ps}\end{figure}$

**図6:** 順圧平均流・傾圧成分から順圧渦成分へのエネルギー変換の時間変化。
凡例中の矢印 "->" はエネルギーの変換を示している。
$\begin{figure}\includegraphics[trim=10 8 0 18,clip,scale=0.62]{img/energy/convers.ps}\end{figure}$

**図7:** 順圧平均流・順圧渦(波数2以上)・傾圧成分から順圧渦成分(波数1)へのエネルギー変換の時間変化。
凡例中の Barotropic Wave 1 は順圧の波数1成分を表す。
$\begin{figure}\includegraphics[trim=10 8 0 18,clip,scale=0.62]{img/energy/convers2-BW1.ps}\end{figure}$

図6において、時刻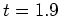以降の傾圧成分から順圧渦成分へのエネルギー変換は、図5の同時刻の順圧渦成分の運動エネルギーのわずかな増加に対応している。この原因を見るために、更に運動エネルギーやエネルギー変換を波数成分ごとに分解して見たのが以下の図である。

図8,10はそれぞれ順圧,傾圧成分の波数ごとの運動エネルギーの時間変化を示したものであり、図9,11はそれぞれ図8,10を拡大したものである。図9,11より、時刻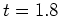頃にロールが壊れ始めてから最初に発達するのは波数4,5の成分である。ロール状対流になって定常的になっている場が傾圧成分を持っているため、この波数4,5は傾圧成分と順圧成分を両方持っている。ただし、約5倍ほど傾圧成分の方が大きい。エネルギーを対数目盛りでプロットした図12におけるグラフの傾きより、波数4,5の順圧・傾圧成分の発達率は約21～23であり(図12はエネルギーの時間変化を示しているので、モードの振幅の発達率に対応させるためには、傾きの1/2を取らなければいけないことに注意)、これは4.1節の線形安定性解析で求めた波数4,5の固有モードの発達率と整合的である。よって、時刻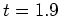頃の順圧渦成分の運動エネルギーのわずかな増加は、波数4,5の固有モードの発達を表していると考えられる。

一方、図12より、遅れて発達してくる波数1の順圧・傾圧成分の擾乱の発達率は約38～46であり、これは4.1節で求めた波数1の固有モード(発達率が8程度)には対応しない。波数1成分の発達率が波数4,5の発達率のおよそ2倍であることから、この波数1成分は波数4成分と波数5成分の重ね合わせによって生成されたと考えられる。すなわち、時刻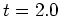以前の波数1の発達は順圧不安定によるものではない。

図13は時刻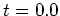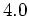～の波数1,4,5の順圧・傾圧成分の時間変化をまとめたものである。ここまでの図で見てきたように、時刻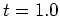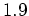～における波数4,5の発達と、その重ね合わせによる波数1の急激な発達(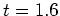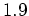～)、さらにその後の波数1の順圧成分の発達(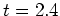以降)、が見てとれる。ここで、時刻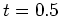までに各成分の指数関数的発達が見られるが、これはシア流に対して傾いたロールの一時的な発達(傾圧成分)と傾圧成分同士の重ね合わせによって生成される順圧成分が見えているものである。

**図8:** 順圧成分の各波数(0,1～6)の運動エネルギーの時間変化。凡例中の Barotropic Wave の後ろの数字は順圧成分の波数を表す。なお、順圧平均流成分については左側の目盛を、順圧渦の各波数成分(1～6)については右側の目盛を読むこと。
$\begin{figure}\includegraphics[trim=12 8 0 18,clip,scale=0.62]{img/energy/energy-BB.ps}\end{figure}$

**図9:** 順圧成分の各波数(0,1～6)の運動エネルギーの時間変化 (図8を拡大)
$\begin{figure}\includegraphics[trim=12 8 0 18,clip,scale=0.62]{img/energy/energy-BB-zoom.ps}\end{figure}$

**図10:** 傾圧成分の各波数(0,1～6)の運動エネルギーと、ポテンシャルエネルギーの時間変化。凡例中の Baroclinic Wave の後ろの数字は傾圧成分の波数、Potential Energy はポテンシャルエネルギーを表す。
$\begin{figure}\includegraphics[trim=10 8 0 18,clip,scale=0.62]{img/energy/energy-CC.ps}\end{figure}$

**図11:** 傾圧成分の各波数(0,1～6)の運動エネルギーの時間変化 (図10を拡大)
$\begin{figure}\includegraphics[trim=12 8 0 18,clip,scale=0.62]{img/energy/energy-CC-zoom.ps}\end{figure}$

**図12:** 順圧・傾圧成分の波数1,4,5の運動エネルギーの時間変化 ( 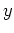軸: 対数目盛り)
実線が順圧成分、破線が傾圧成分を表している。
$\begin{figure}\includegraphics[trim=12 8 0 10,clip,scale=0.62]{img/energy/energy-BBCC-log.ps}\end{figure}$

**図13:** 順圧・傾圧成分の波数1,4,5の運動エネルギーの時間変化 ( 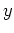軸: 対数目盛り)
$\begin{figure}\includegraphics[trim=10 8 0 12,clip,scale=0.62]{img/energy/energy-BBCC-log6.ps}\end{figure}$

SAITO Naoaki
2008-03-07