5.3.3 浮力偏差の生成への寄与
更に、浮力偏差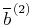 の生成要因について調べる。(18)の右辺第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、右辺の総和の
の生成要因について調べる。(18)の右辺第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、右辺の総和の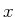 -
-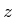 分布は図31(
分布は図31( の場合は図33)のようになる。等高線間隔から読み取れるように、第1項の熱輸送の効果の寄与が最も大きい。更に、
の場合は図33)のようになる。等高線間隔から読み取れるように、第1項の熱輸送の効果の寄与が最も大きい。更に、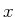 -
-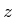 面における熱フラックス
面における熱フラックス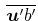 を図32(
を図32(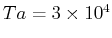 の場合は図34)に示す。これを見ると、
の場合は図34)に示す。これを見ると、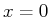 付近にある上向きの熱フラックスが図31(
付近にある上向きの熱フラックスが図31(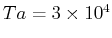 の場合は図33)の一番上の図に見られる上下の浮力偏差を生むのが分かる。すなわち、固有モードの擾乱による鉛直上向きの熱輸送が浮力偏差の生成に大きく寄与する。
の場合は図33)の一番上の図に見られる上下の浮力偏差を生むのが分かる。すなわち、固有モードの擾乱による鉛直上向きの熱輸送が浮力偏差の生成に大きく寄与する。
第1項 (CONTOUR INTERVAL
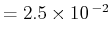
)
第2項 (CONTOUR INTERVAL
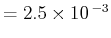
)
第3項 (CONTOUR INTERVAL
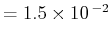
)
総和 (CONTOUR INTERVAL
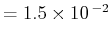
)
図31:
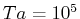 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、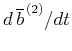 への各項の寄与。上から順に、
への各項の寄与。上から順に、
第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、総和。
|
図32:
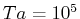 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、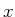 -
-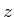 面における熱フラックス
面における熱フラックス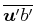
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 210 0,clip,scale=0.65]{img2/ksA-ph15-f316-e-bflux.ps}\end{center}\end{figure}](img303.png)
|
第1項 (CONTOUR INTERVAL
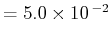
)
第2項 (CONTOUR INTERVAL
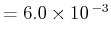
)
第3項 (CONTOUR INTERVAL
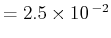
)
総和 (CONTOUR INTERVAL
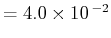
)
図33:
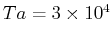 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、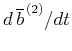 への各項の寄与。上から順に、
への各項の寄与。上から順に、
第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、総和。
|
図34:
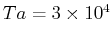 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、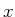 -
-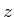 面における熱フラックス
面における熱フラックス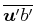
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 210 0,clip,scale=0.65]{img2/ksA-ph15-f173-e1-bflux.ps}\end{center}\end{figure}](img312.png)
|
SAITO Naoaki
2009-07-09
![]() の生成要因について調べる。(18)の右辺第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、右辺の総和の
の生成要因について調べる。(18)の右辺第1項(擾乱同士の相互作用: 熱輸送の効果)、第2項(鉛直流の効果)、第3項(拡散の効果)、右辺の総和の![]() -
-![]() 分布は図31(
分布は図31(![]() の場合は図33)のようになる。等高線間隔から読み取れるように、第1項の熱輸送の効果の寄与が最も大きい。更に、
の場合は図33)のようになる。等高線間隔から読み取れるように、第1項の熱輸送の効果の寄与が最も大きい。更に、![]() -
-![]() 面における熱フラックス
面における熱フラックス![]() を図32(
を図32(![]() の場合は図34)に示す。これを見ると、
の場合は図34)に示す。これを見ると、![]() 付近にある上向きの熱フラックスが図31(
付近にある上向きの熱フラックスが図31(![]() の場合は図33)の一番上の図に見られる上下の浮力偏差を生むのが分かる。すなわち、固有モードの擾乱による鉛直上向きの熱輸送が浮力偏差の生成に大きく寄与する。
の場合は図33)の一番上の図に見られる上下の浮力偏差を生むのが分かる。すなわち、固有モードの擾乱による鉛直上向きの熱輸送が浮力偏差の生成に大きく寄与する。![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f316-e-FXb-2.ps}
\end{center}\end{figure}](img298.png)
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f316-e-FXb-3.ps}
\end{center}\end{figure}](img300.png)
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f316-e-FXb-4.ps}
\end{center}\end{figure}](img302.png)
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f173-e1-FXb-2.ps}
\end{center}\end{figure}](img306.png)
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f173-e1-FXb-3.ps}
\end{center}\end{figure}](img308.png)
![\begin{figure}\begin{center}
\protect\includegraphics[trim=155 0 190 0,clip,scale=0.5]{img2/ksA-e-FX/f173-e1-FXb-4.ps}
\end{center}\end{figure}](img310.png)